1.3.2三角函数的图像和性质2-LeeVIP免费

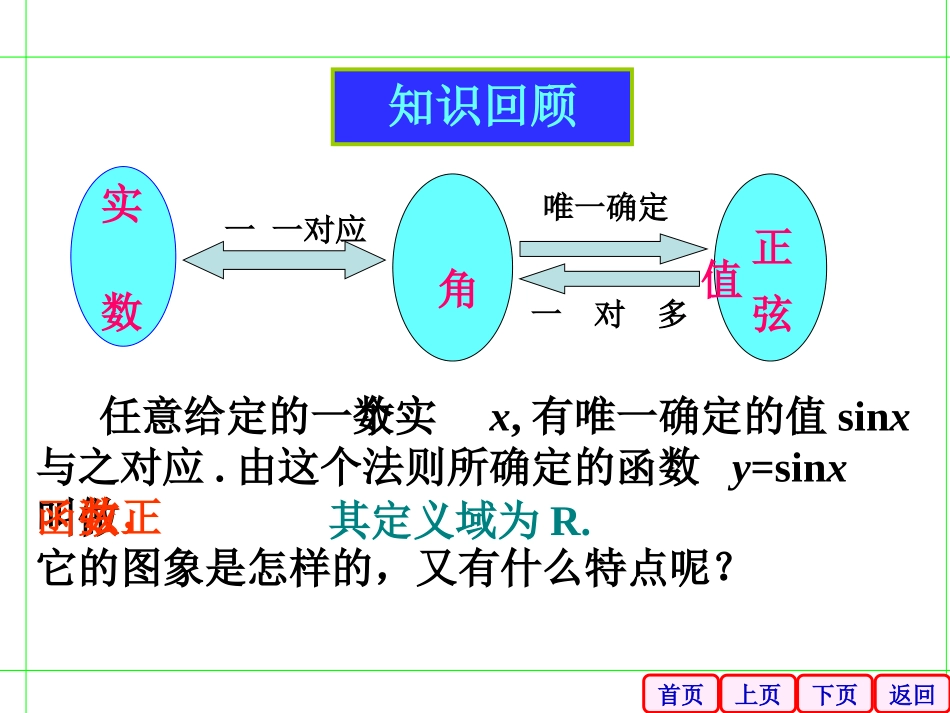
1.3.2三角函数的图像和性质首页上页返回下页实数正弦值角一一对应唯一确定任意给定的一个实数x,有唯一确定的值sinx与之对应.由这个法则所确定的函数y=sinx叫做正弦函数，它的图象是怎样的，又有什么特点呢？其定义域为R.一对多知识回顾首页上页返回下页知识回顾1.sinα、cosα、tanα的几何意义:oxy11PMAT正弦线MP余弦线OM正切线AT代数问题几何问题首页上页返回下页知识回顾(1)列表(2)描点(3)连线2.用描点法作出函数图象的主要步骤是怎样的？首页上页返回下页O1怎样在直角坐标系中作出(x0,sinx0)?xy1-1OPMAx0x0(x0,sinx0)MP=sinx0首页上页返回下页O1xyO1-1-1步骤:作图过程演示3232656734233561126(1)等分(2)作正弦线(3)平移(4)连线思考：如何作出y=sinx在[2π,4π]的图象？首页上页返回下页------01-1xy2π4π-2π-4π6π-6π正弦曲线正弦函数的图象叫做正弦曲线xyO逆时针旋转顺时针旋转首页上页返回下页------01-1xy2π4π-2π-4π6π-6π正弦曲线正弦函数的图象叫做正弦曲线xyO逆时针旋转顺时针旋转首页上页返回下页与x轴的交点)0,0()0,()0,2(图象的最高点)1,(2图象的最低点)1(,23(1)列表(列出对图象起关键作用的五点坐标)(2)描点(定出五个关键点)(3)连线(用光滑曲线顺次连结五点)3.五点作图法问题：图象中的关键点有哪些？首页上页返回下页y--------1-12o46246xycos由于余弦曲线4.余弦函数的图像正弦曲线2所以余弦函数的图像可以通过正弦曲线向左平移)2sin(xx个单位长度而得到．首页上页返回下页与x轴的交点)0,0()0,()0,2(图象的最高点)1,(2图象的最低点)1(,23与x轴的交点)0,(2)0,(23图象的最高点)1,0(图象的最低点)1,(简图作法(五点作图法)(1)列表(列出对图象形状起关键作用的五点坐标)(2)描点(定出五个关键点)(3)连线(用光滑的曲线顺次连结五个点)sinyxcosyx首页上页返回下页xyo-例1用五点法作图（1）作出函数y=sinx+1,x[0,2π]∈的图.解:按五个关键点列表求值描点作图-2223211-xxsin1sinx101010210102232注：函数y=sinx+1，x[0,2π]∈的图象可通过把函数y=sinx，x[0,2π]∈图象上的每一点向上平移1个单位长度得到。y=sinx+1y=sinx首页上页返回下页yx-101π2π223（2）作出函数y=-cosx,x∈[0,2π]的简图。解:按五个关键点列表求值描点作图02232注：函数y=-cosx，x[0,2π]∈的图象与函数y=cosx，x[0,2π]∈图象关于x轴对称。xxcosxcosxycosxycos1-11-100-1100首页上页返回下页（3）作出函数y=2cosx,的简图。解:按五个关键点列表求值描点作图02232注：函数y=2cosx的图像可以看做是函数y=cosx的图象上所有点的纵坐标变为原来的2倍（横坐标不变）而得到的。xxcos2cosxxycos2cosyx12100-1002202-22322322xRyx首页上页返回下页（4）作出函数y=sin2x,的简图。解:按五个关键点列表求值描点作图x2xsin2xsinyxsin2yx001-102xR0023220423423221-1yx434首页上页返回下页正弦、余弦函数y=sinx,y=cosx,x∈R的图象2o46246xy---------1-12o46246xy---------1-1正弦曲线余弦曲线首页上页返回下页函数性质y=sinxy=cosx定义域值域最值及相应的x的集合(k∈Z)奇偶性RR[-1,1][-1,1]x=2kπ时,ymax=1x=2kπ+π时,ymin=-1奇函数偶函数x=2kπ+时,ymax=1x=2kπ-时,ymin=-1π2π2首页上页返回下页例2求下列函数的最大值及取得最大值时自变（1）cos3xy解：函数的最大值为1，因为使令3xz，由23xk，得6xk.所以，使函数cos3xy取得最大值的x的集合为：取得最大值的z的集合为},2|{Zkkzz量x的集合：cos3xyzcos}.,6|{Zkkxx首页上页返回下页（2）2sin2yx2sin2yxsinz解：函数的最大值为2－(－1)=3.因为使取得最小值的z的集合为：令2zx，由222xk，得4xk。所以，使函数2sin2yx取得最大值的x的集合为：.,22|Zkkzz.,4|Zkkxx首页上页返回下页作业教材P32练习2、3、4；P44习题1.32、3、4．