圆锥的侧面积和全面积MEVIP免费

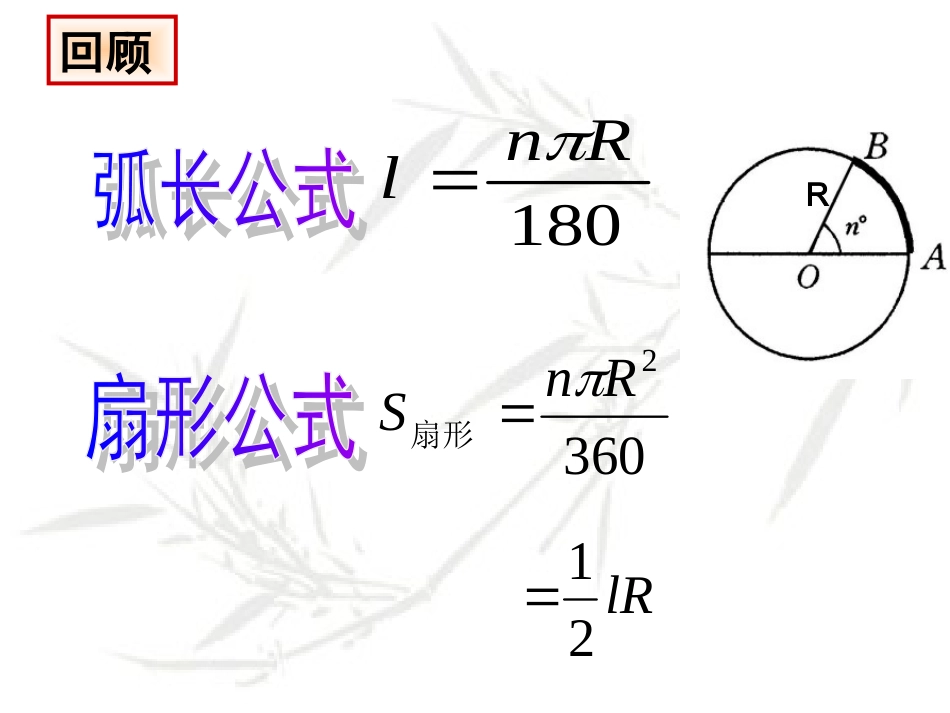
24.4圆中的计算问题回顾180Rnl3602RnS扇形lR21R•认识圆锥生活中的圆锥OPABrha1.圆锥是由一个底面和一个侧面围成的,它的底面是一个圆,侧面是一个曲面.2.把圆锥底面圆周上的任意一点与圆锥顶点的连线叫做圆锥的母线.如图中的a.3.连结顶点与底面圆心的线段叫做圆锥的高.如图中的h.圆锥的母线有几条？圆锥的再认识无数条图23.3.7圆锥的认识ahr圆锥的底面半径、高线、母线长三者之间的关系:222rha55．把圆锥模型沿着母线剪开，．把圆锥模型沿着母线剪开，观察圆锥的侧面展开图．观察圆锥的侧面展开图．探究4.圆锥的形成过程5.圆锥的侧面积和全面积问题问题::1、沿着圆锥的母线，把一个圆锥的侧面展开，得到一个扇形，这个扇形的弧长与底面的周长有什么关系？2、圆锥侧面展开图是扇形，这个扇形的半径与圆锥中的哪一条线段相等？图23.3.7相等母线探究lrhaS侧=S扇形S全=S侧+S底圆锥的侧面积和全面积圆锥的底面周长就是其侧面展开图扇形的弧长，圆锥的母线就是其侧面展开图扇形的半径。rarala221212rra探究1.圆锥的侧面展开图是一个扇形2.圆锥的底面圆周长就是其侧面展开图扇形的弧长3.圆锥的母线就是其侧面展开图扇形的半径。ahr圆锥的侧面展开图：4.圆锥的侧面积就是弧长为圆锥底面的周长、半径为圆锥的一条母线的长的扇形面积.5.圆锥的全面积=侧面积+底面积.演示你会计算展开图中的圆心角的度数吗？lrha思考：180anlaln1801、填空根据下列条件求值（其中r、h、a分别是圆锥的底面半径、高线、母线长）（1）a=2，r=1则h=_______(2)h=3,r=4则a=_______(3)a=10,h=8则r=_______3562、根据圆锥的下面条件，求它的侧面积和全面积（1）r=12cm,a=20cm（2）h=12cm,r=5cm（1）侧：240π全：384π（2）侧：65π全：90π3、填空、根据下列条件求圆锥侧面积展开图的圆心角（r、h、a分别是圆锥的底面半径、高线、母线长）（1）a=2，r=1则=________(2)h=3,r=4则=__________rha180°288°1、圆锥的侧面展开图2、计算圆锥的侧面积和全面积，3、圆锥的底面周长就是其侧面展开图扇形的弧长。4、圆锥的母线就是其侧面展开图扇形的半径ahrOPABrha圆锥的侧面积S侧=πraahr圆锥的全面积圆锥的侧面积和全面积2、如图，若圆锥的侧面展开图是半圆，那么这个展开图的圆心角是___度；圆锥底半径r与母线a的比r：a=___.1801:2lrhSBAO1、如果圆锥的底面周长是20π,侧面展开后所得的扇形的圆心角为120度,则该圆锥的侧面积为_____,全面积为_______300π400π２圆锥的母线与高的夹角为30°，母线长为6cm,它的全面积为＿＿，27π童心玩具厂欲生产一种圣诞老人的帽子，其帽身是圆锥形(如图)PB=15cm，底面半径r=5cm，生产这种帽身10000个，你能帮玩具厂算一算至少需多少平方米的材料吗（不计接缝用料，和余料,π取3.14，）？APBOrl.答：至少需235.5平方米的材料.如图，圆锥的底面半径为1，母线长为6，一只蚂蚁要从底面圆周上一点B出发，沿圆锥侧面爬行一圈再回到点B，问它爬行的最短路线是多少？ABCABC作过点AC，BDB圆锥的底面半径、高线、母线长三者之间有什么关系?222rhaOPABrha思考a、h、r构成一个直角三角形圆柱侧面展开图1.圆柱的侧面展开图是一个矩形,它的一边长是圆柱的母线长;它的另一边长是圆柱的底面圆周长。2.圆柱的侧面积是母线与圆柱的底面圆周长围成的矩形面积。3.圆柱的全面积=侧面积+底面积回顾例1、一个圆锥形零件的母线长为a，底面的半径为r，求这个圆锥形零件的侧面积和全面积．解:圆锥的侧面展开后是一个扇形，该扇形的半径为a，扇形的弧长为2πr，所以S侧＝S底＝πr2；S＝πra＋πr2．答：这个圆锥形零件的侧面积为πra，全面积为πra＋πr221×2πr×a＝πra1.圆锥的侧面展开图是一个扇形2.圆锥的底面圆周长就是其侧面展开图扇形的弧长3.圆锥的母线就是其侧面展开图扇形的半径。ahr课堂小结：4.圆锥的侧面积就是弧长为圆锥底面的周长、半径为圆锥的一条母线的长的扇形面积.5.圆锥的全面积=侧面积+底面积.演示