浙江省杭州地区七校高三数学第三次质量检测试题 文-人教版高三全册数学试题VIP免费

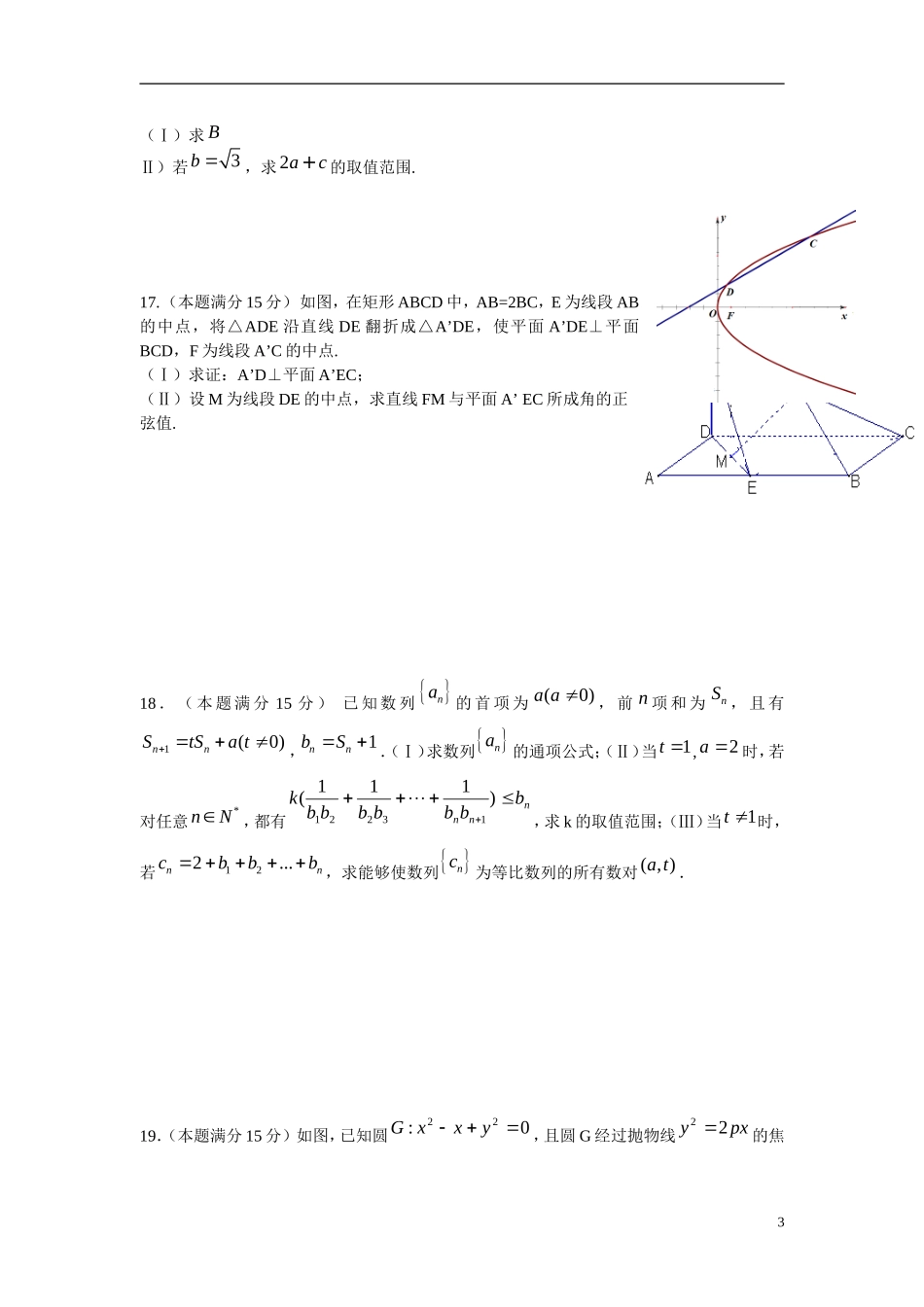
2014学年杭州地区七校高三第三次质量检测数学（文）试题考生须知：1．本卷满分150分，考试时间120分钟；2．答题前，在答题卷密封区内填写班级、学号和姓名；座位号写在指定位置；3．所有答案必须写在答题卷上，写在试卷上无效；4．考试结束后，只需上交答题卷。选择题（每题5分，共40分）1.已知a，b都是实数，那么“ab”是“a>b”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件2.设l是直线，，β是两个不同的平面，则下列判断正确的是()A.若l∥，l∥β，则∥βB.若⊥β,l∥，则l⊥βC.若⊥β，l⊥，则l⊥βD.若l⊥，l⊥β，则∥β3.下列函数中，满足“fxyfxfy”的单调递减函数是（）A.12fxxB.3fxxC.12xfxD.3xfx4.函数cos(2)6yx的图象可由函数sin2yx的图象（）A.向左平移3个单位而得到B.向右平移3个单位而得到C.向左平移6个单位而得到D.向右平移6个单位而得到5.直角三角形ABC中，A为直角，AB=1，BC=2，，若点AM是BC边上的高线，点P在ABC内部或边界上运动，则AMBP�的范围是（）A.3[,0]2B.3[,0]4C.3[,0]4D.[3,0]6.设1sin20nnan，nnaaaS21，在1280,,,SSS中，正数的个数是（）A．20B．40C．60D．8017.双曲线22221(0,0)xyabab的左、右焦点分别为12,FF,渐近线分别为12,ll，点P在第一象限内且在1l上，若2122,//lPFlPF，则双曲线的离心率是（）A．5B.2C.3D.28.已知21fxx，若直线ym与函数yffx的图象有四个不同的交点，则实数m的取值范围是（）A.1,2B.0,3C.1,1D.1,3填空题9.已知集合M={x|y=lg[(x-2)(x+1)]}，N={y|+1yx}，为实数集，则M∩N=，MN,RCM.10.函数12cos()32yx，则该函数的最小正周期为，对称轴方程为，单调递增区间是.11.某四面体的三视图如图所示，该四面体的体积是,该四面体四个面的面积中最大的是.12.设1,m在线性约束条件1yxymxxy下，目标函数5zxy的最大值为4，则m的值为．此时，约束条件下的平面区域的面积为.13.设12(0)()(1)2(0)xxfxfxx，则2015()2f.14.在平面直角坐标系xOy中，圆C的方程为228150xyx，若直线2ykx上至少存在一点，使得以该点为圆心，1为半径的圆与圆C有公共点，则k的最大值是．15.设正实数x,y,z满足4,5xyzxyyzzx，则y的取值范围为.解答题16.（本题满分15分）在ABC中，角A，B，C的对边分别为a，b，c，已知cos3sin0bCbCac.2（Ⅰ）求BⅡ）若3b，求2ac+的取值范围.17.（本题满分15分）如图，在矩形ABCD中，AB=2BC，E为线段AB的中点，将△ADE沿直线DE翻折成△A’DE，使平面A’DE⊥平面BCD，F为线段A’C的中点.（Ⅰ）求证：A’D⊥平面A’EC；（Ⅱ）设M为线段DE的中点，求直线FM与平面A’EC所成角的正弦值.18．（本题满分15分）已知数列na的首项为(0)aa，前n项和为nS，且有1(0)nnStSat，1nnbS．（Ⅰ）求数列na的通项公式；（Ⅱ）当1t,2a时，若对任意*nN，都有nnnbbbbbbbk)111(13221，求k的取值范围；（Ⅲ）当1t时，若122...nncbbb，求能够使数列nc为等比数列的所有数对(,)at．19．（本题满分15分）如图，已知圆0:22yxxG，且圆G经过抛物线pxy22的焦3点，过点)0,(m)0(m倾斜角为6的直线l交抛物线于C，D两点.（Ⅰ）求抛物线的方程；（Ⅱ）若焦点F在以线段CD为直径的圆E的外部，求m的取值范围．20.（本题满分14分）已知函数()fx和()gx的图象关于原点对称，2()2fxxx.（1）若函数1()()22hxfxxxa有四个不同零点，求实数a的取值范围（2）如果对于任意xR，不等式()()1gxcfxx恒成立，求实数c的取值范围42014学年杭州地区七校高三第三次质量检测数学（文科）参考答案最终定稿人：萧山十中李兆贵联系电话：18958156537一选择题（每题5分，共40分）1.已知a，b都是实数，那么“ab”是“a>b”的(D)A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分...