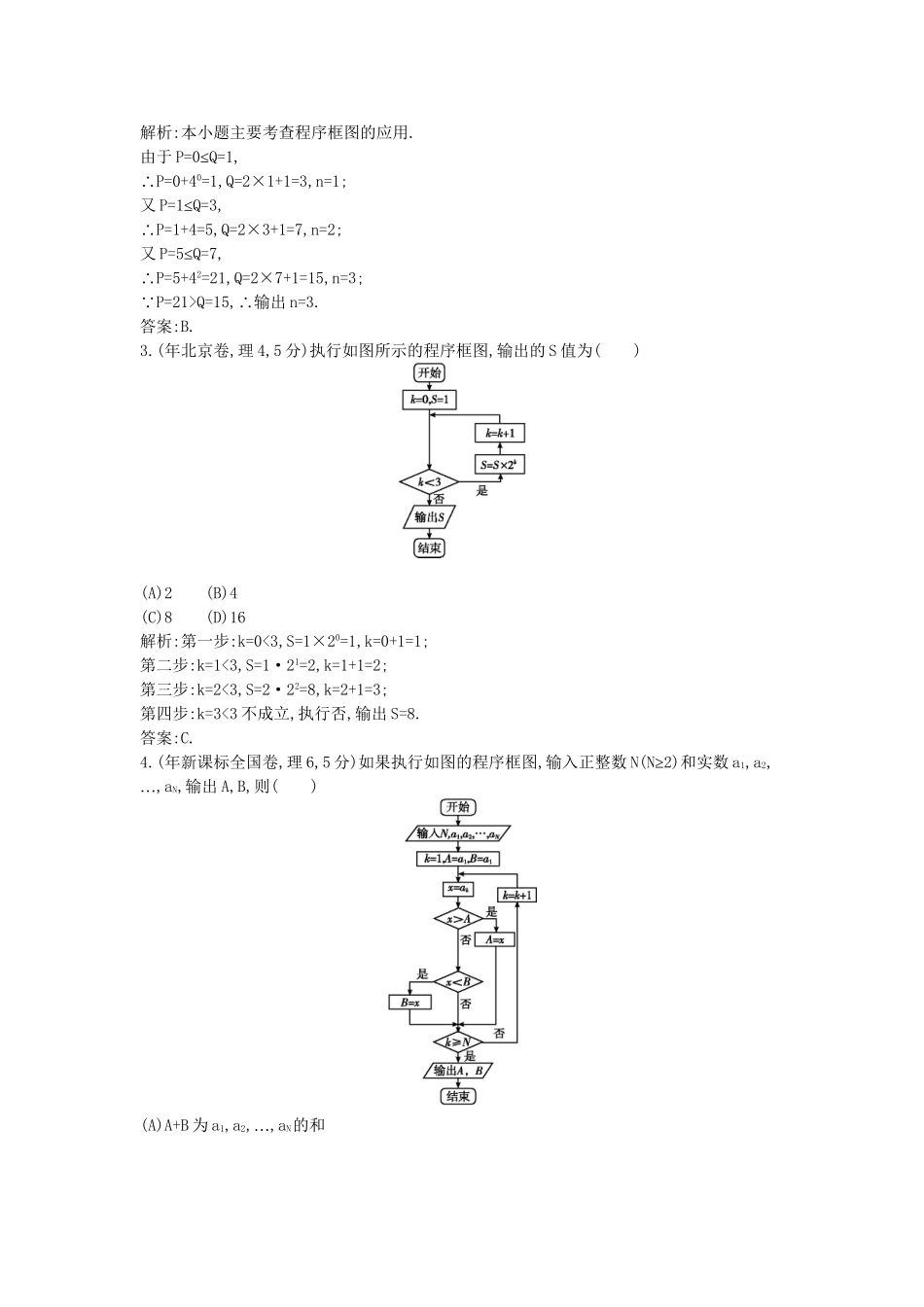
第一节算法初步程序框图的输出功能考向聚焦算法初步是新课标的新增内容,是高考的一个必考点,程序框图是考查的重点,特别是以循环结构为主的程序框图.程序框图常与分段函数求值、数据的大小关系、数列求和或求积、统计与概率等知识联系在一起,有的是输出计算次数、有的是输出计算结果,多以选择题、填空题的形式出现,一般为中等偏易题,所占分值4~5分备考指津复习考点应放在读懂框图上,尤其是循环结构,因为一个程序框图中只要有了循环结构,那么一定会涉及条件结构和顺序结构.对于循环结构,要注意当型与直到型的区别,搞清进入或退出的循环条件、循环次数,是做对题的关键1.(年安徽卷,理3,5分)如图所示,程序框图(算法流程图)的输出结果是()(A)3(B)4(C)5(D)8解析:本题考查程序框图的识别.第一次运算后,x=2,y=2,第二次运算后,x=4,y=3,第三次运算后,x=8,y=4,输出的结果为y的值,是4.答案:B.2.(年山东卷,理6,5分)执行下面的程序框图,如果输入a=4,那么输出的n的值为()(A)2(B)3(C)4(D)5解析:本小题主要考查程序框图的应用.由于P=0≤Q=1,∴P=0+40=1,Q=2×1+1=3,n=1;又P=1≤Q=3,∴P=1+4=5,Q=2×3+1=7,n=2;又P=5≤Q=7,∴P=5+42=21,Q=2×7+1=15,n=3; P=21>Q=15,∴输出n=3.答案:B.3.(年北京卷,理4,5分)执行如图所示的程序框图,输出的S值为()(A)2(B)4(C)8(D)16解析:第一步:k=0<3,S=1×20=1,k=0+1=1;第二步:k=1<3,S=1·21=2,k=1+1=2;第三步:k=2<3,S=2·22=8,k=2+1=3;第四步:k=3<3不成立,执行否,输出S=8.答案:C.4.(年新课标全国卷,理6,5分)如果执行如图的程序框图,输入正整数N(N≥2)和实数a1,a2,…,aN,输出A,B,则()(A)A+B为a1,a2,…,aN的和(B)为a1,a2,…,aN的算术平均数(C)A和B分别是a1,a2,…,aN中最大的数和最小的数(D)A和B分别是a1,a2,…,aN中最小的数和最大的数解析:易知A、B分别为a1,a2,…,aN中的最大数和最小数,应选C.答案:C.5.(年天津卷,理3,5分)阅读如图所示的程序框图,运行相应的程序,当输入x的值为-25时,输出x的值为()(A)-1(B)1(C)3(D)9解析:本小题考查程序框图.当输入x=-25时,|x|>1,因此执行x=-1=-1=4,由于|4|>1,故执行x=-1=-1=1,而x=1时,不满足|x|>1,所以执行x=2x+1=2×1+1=3.故选C.答案:C.6.(年辽宁卷,理9,5分)执行如图所示的程序框图,则输出的S值是()(A)-1(B)(C)(D)4解析:→→→→,显然S的取值以4为周期重复出现,∴i=9时,输出S=4.故选D.答案:D.7.(年陕西卷,理8)如图中,x1,x2,x3为某次考试三个评阅人对同一道题的独立评分,p为该题的最终得分.当x1=6,x2=9,p=8.5时,x3等于()(A)11(B)10(C)8(D)7解析:开始输入x1,x2, |x1-x2|=|6-9|=3>2,∴执行否,输入x3.若|x3-x1|<|x3-x2|成立即执行是,结果p==8.5,则x3=11,与|x3-x1|<|x3-x2|矛盾.若|x3-x1|<|x3-x2|不成立即执行否,则p==8.5,则x3=8符合条件,∴x3=8.故选C.答案:C.8.(年北京卷,理4)执行如图所示的程序框图,输出的s值为()(A)-3(B)-(C)(D)2解析: i=0<4,∴i=1,s==, i=1<4,∴i=2,s==-, i=2<4,∴i=3,s==-3, i=3<4,∴i=4,s==2, i=4<4不成立,∴输出的s=2,故选D.答案:D.9.(年全国新课标卷,理3)执行如图所示的程序框图,如果输入的N是6,那么输出的p是()(A)120(B)720(C)1440(D)5040解析: N=6,当k=1,p=1时,p=1,则k50,所以输出i=4,故选B.答案:B.11.(年辽宁卷,理6)执行如图的程序框图,如果输入的n是4,则输出的p是()(A)8(B)5(C)3(D)2解析:k=1时,p=1,s=1,t=1;k=2