反比例函数的性质及应用VIP免费

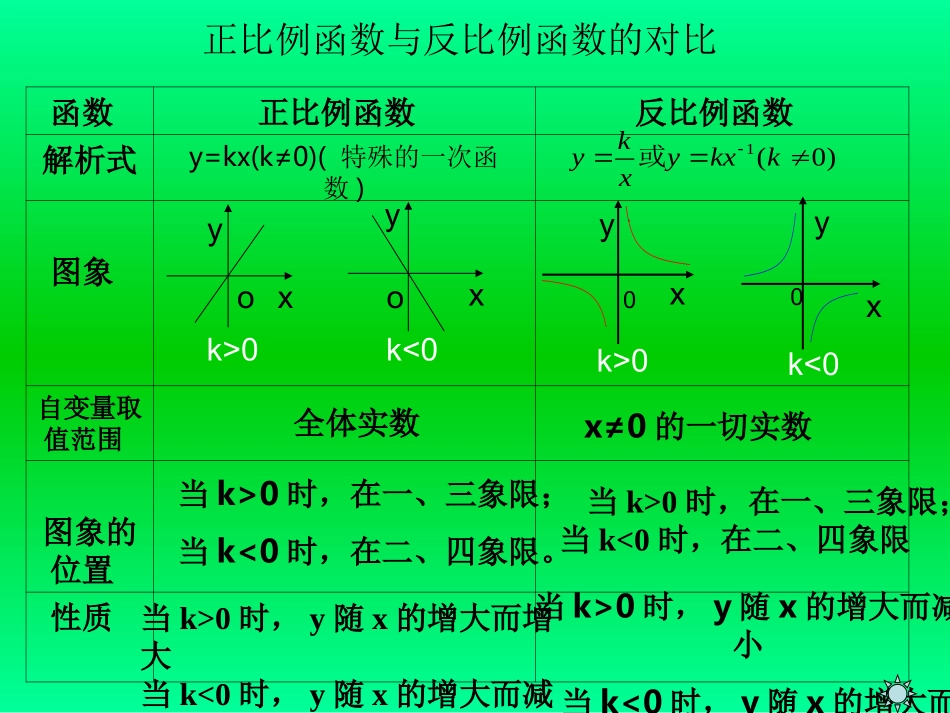
温顾知新学以致用规律总结初显身手中考导航一函数正比例函数反比例函数解析式图象自变量取值范围图象的位置性质当k>0时，y随x的增大而减小当k<0时，y随x的增大而增大正比例函数与反比例函数的对比y=kx(k≠0)(特殊的一次函数)全体实数x≠0的一切实数当k>0时，在一、三象限；当k<0时，在二、四象限。当k>0时，在一、三象限；当k<0时，在二、四象限当k>0时，y随x的增大而增大当k<0时，y随x的增大而减小k<0xyoxyok>0k<0yx0y0k>0x)0(1kkxyxky或二.____,)0()0(.12112象是直角坐标系内的大致图那么它们在同一的增大而增大随的函数值都比例函数与反若正比例函数xkykxkyxkOxyACOxyDxyoOxyBD....,.0,0..____,,2)2000.(2四象限图象在第二三象限图象在第一的增大而减小随在每个象限内时当反比例函数那么的增大而减小随已知一次函数年河南、D。、CxyByxAxkyxykxyyOxD四象限三第二四象限三第一四象限二第一三象限二第的图象经过那么一次函数而增大的增大随时当已知反比例函数年四川、、D、、C、、B、、Akkxyxyxkxky....._____,,0),0()2000.(3xyoB.____)0()1()1999.(4图象的是在同一坐标系中的大致和如图能表示年哈尔滨kxkyxkyOxyACOxyDxyoOxyBD.____,)1999.(52的图像大致为与函数在同一坐标系中年黑龙江xbybxaxyOxyAOxyDCxyoOxyBD二三则垂足为轴的垂线作过有一点上任意是双曲线设,,)1(,)0(),(AxPkxkynmP||21||||2121knmAPOASOAPP(m,n)AoyxP(m,n)AoyxP(m,n)AoyxP(m,n)Aoyx想一想若将此题改为过P点作y轴的垂线段,其结论成立吗?||21||||2121knmAPOASOAP.||||||,,,,)2(knmAPOASBAyxPOAPB矩形则垂足分别为轴的垂线轴分别作过P(m,n)AoyxBP(m,n)AoyxB.||2|2||2|21||21,),,(),()3(knmPAAPSAyPxPnmPnmPPPA则点轴的垂线交于作轴的垂线与过作过关于原点的对称点是设P(m,n)AoyxP/P(m,n)oyxP/yP(m,n)oxP/以上几点揭示了双曲线上的点构成的几何图形的一类性质.掌握好这些性质,对解题十分有益.(上面图仅以P点在第一象限为例).四.___,,.,.,)2000.(621则的面积为的面积为记垂足为轴的垂线作过垂足为轴的垂线作过年武汉市SRtSRtDyCBxAOCDAOB如图:A、C是函数的图象上任意两点，xy1A.S1>S2B.S12.___,,,,1,,7则面积为的轴平行于轴平行于的任意两点对称的图图像上关于原点是函数如图SABCxBCyACOxyBA、ACoyxB∴选C解:由上述性质(3)可知,SABC△=2|k|=2C.,,21||21,21||21,21||21321111ASSSkSkSkSOOCBOBAOA故选即解:由性质(1)得A.__,,,,,,,,,,,,,,,)0(1,8321111111则有面积分别为的记边结三点轴于交轴引垂线经过三点分别向的图像上有三点在如图SSSOCCOBBOAAOCOBOACBAxxCBAxxy、A.S1=S2=S3B.S1S2>S3BA1oyxACB1C1S1S3S23k.3|||,|kkSAPCO矩形,,四象限图像在二又.____,3,,,,.9函数的解析式是则这个反比例阴影部分面积为轴引垂线轴向分别由图像上的一点是反比例函数如图yxPxkyPACoyxP.3xy解析式为解:由性质(2)可得五.1.,,)0(,,,)0(,)2003.(1ODOBOADxCDCCmxmyBAyxkbkxy若垂足为轴垂直于作过点象交于点的图且与反比例函数两点分别交于轴轴的图象与已知一次函数如图年天津.)2(;,,)1(数的解析式求一次函数和反比例函的坐标求点DBAABCyxDO.2,8)1(:xyxy解.4,2;2,4yxyx或解得).2,4(),4,2(BA.)2(;,)1(.,28,.2的面积两点的坐标求两点交于的图像与一次函数反比例函数已知如图AOBBABAxyxyAyOBxMNAyOBxMN.642OAMOMBAOBSSS).0,2(,2,0,2:)2(Mxyxy时当解法一.2OM.,DxBDCxAC轴于轴于作,2,4BDAC,2222121BDOMSOMB.4422121ACOMSOMACDAyOBxMN.624ONAONBAOBSSS).2,0(,2,0,2:)2(Nyxxy时当解法二.2ON.,DyBDCyAC轴于轴于作,4,2BDAC,44...