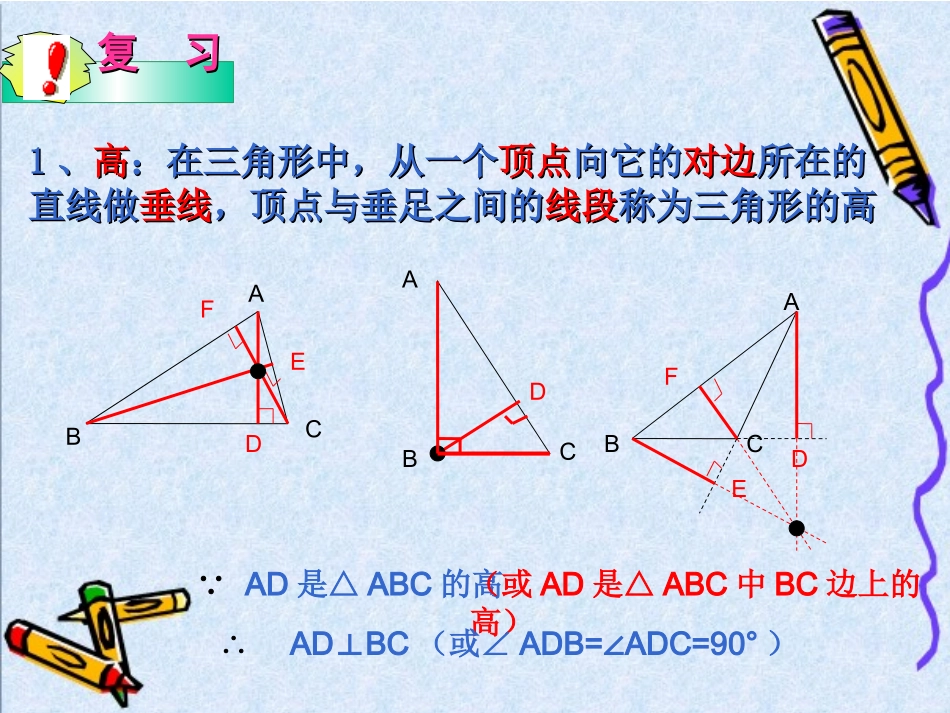
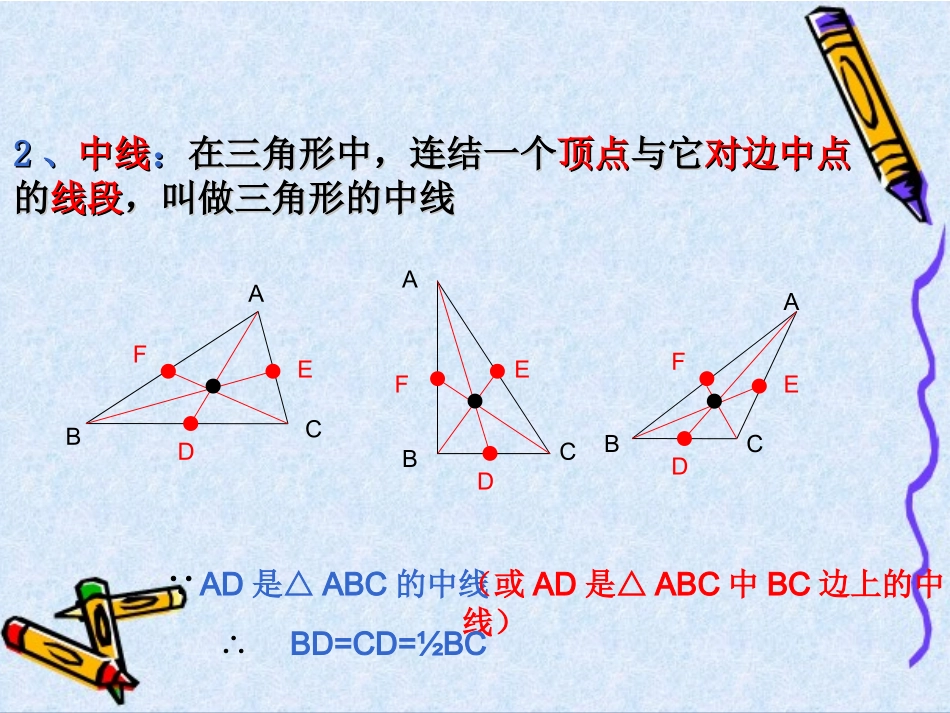
复习复习11、、高高:在三角形中,从一个:在三角形中,从一个顶点顶点向它的向它的对边对边所在的所在的直线做直线做垂线垂线,顶点与垂足之间的,顶点与垂足之间的线段线段称为三角形的高称为三角形的高ABCDAD是△ABC的高(或AD是△ABC中BC边上的高)∵∴ADBC⊥(或∠ADB=ADC=90°∠)EFABCDABCDEF22、、中线中线::在三角形中,连结一个在三角形中,连结一个顶点顶点与它与它对边中点对边中点的的线段线段,叫做三角形的中线,叫做三角形的中线ABCFEDAD是△ABC的中线(或AD是△ABC中BC边上的中线)∵∴BD=CD=½BCABCDEFABCFEDABCABCABC33、、角平分线角平分线::在三角形中,一个在三角形中,一个内角的角平分线内角的角平分线与与它它对边对边相交,这个角的相交,这个角的顶点顶点与与交点交点之间的之间的线段线段,叫做,叫做三角形的角平分线三角形的角平分线DEFDEFDFEAD是△ABC的角平分线(或AD是△ABC中∠BAC的角平分线)∵∠BAD=DAC=½BAC∠∠∴课前热身课前热身1、三角形的角平分线、中线、高都是()A、线段B、射线C、直线D、射线或线段A2、要求画△ABC的边AB上的高,下列画法中,正确的是()CEDACB(第1题图)3、在△ABC中,AD是角平分线,BE是中线,∠BAD=40°,则∠CAD=,若AC=6cm,则AE=()4、下列说法正确的是()A、三角形的角平分线、中线、高都在三角形的内部B、直角三角形只有一条高C、三角形的三条高至少有一条在三角形内D、钝角三角形的三条高均在三角形外C40°3cm6cm²5、如图,AD、AE分别是△ABC的中线和高,BC=6cm,AE=4cm,△ABD的面积为(),△ADC的面积为()。6cm²ABCDE试一试试一试1、如图,AE是△ABC的角平分线.已知:∠B=40°,∠C=60°,求∠CAE和∠AEB的大小.ECAB已知:如图,在△ABC中,AD⊥BC,垂足是D,∠B=70°,∠BAC=46°,求∠CAD的度数.ABCD同学甲:∠C=180°-∠B-∠A=180°-70°-46°=64°∠CAD=180°-∠C-∠ADC=180°-64°-90°=26°同学乙:∵∠B=70°,∠BAC=46°∠B+BAC+C=180°∠∠(三角形的内角和等于180°)∴∠C=180°-∠B-∠BAC=180°-70°-46°=64°又∵AD⊥BC∴∠ADC=90°(垂直的定义)∴∠CAD=180°-∠C-∠ADC=180°-64°-90°=26°逻辑思维试一试试一试1、如图,AE是△ABC的角平分线.已知:∠B=40°,∠C=60°,求∠CAE和∠AEB的大小.ECAB解:∵∠B=40°∠C=60°∴∠CAB=180°-∠B-∠C=180°-40°-60°=80°又∵AE是△ABC的角平分线∴∠CAE=∠EAB=∠CAB=40°又∵∠B=40°,∠EAB=40°∴∠AEB=180°-B-EAB∠∠=180°-40°-40°=100°½2、如图,已知:在△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高,试求∠DBC的度数.解:∵∠C=∠ABC=2∠A∠A+∠ABC+∠C=180°∴∠A+2∠A+2∠A=180°即:∠A=36°∴∠C=∠ABC=72°又∵BD是AC边上的高∴∠BDC=90°又∵∠C=72°∴∠DBC=180°-BDC-C∠∠=180°-90°-72°=18°ABCD3、如图,已知:在△ABC中,BD是AC边上的中线,AB=5cm,BC=8cm,试求△CDB和△ABD的周长的差是多少?ADCB解:∵BD是AC边上的中线∴AD=CD又∵AB=5cm,BC=8cm∴△CDB的周长-△ABD的周长=(BC+BD+CD)-(AB+BD+AD)=BC-AB=8-5=3(cm)故△CDB和△ABD的周长的差是3cm.结论:两三角形的周长之差等于两边之差(变式)如图,已知:在△ABC中,BD是AC边上的中线,,△ABD和△BDC的周长的差是5cm,AB边的长为13cm,求BC边的长ACBD8cm如图,在△如图,在△ABCABC中,中,ADAD是△是△ABCABC的的高,高,AEAE是△是△ABCABC的角平分线。已知的角平分线。已知∠∠BACBAC==8888°°,∠,∠BB==5555°°,求∠,求∠DAEDAE的大小。的大小。如图,在△如图,在△ABCABC中,中,ADAD是△是△ABCABC的的高,高,AEAE是△是△ABCABC的角平分线。已知的角平分线。已知∠∠BACBAC==8888°°,∠,∠BB==5555°°,求∠,求∠DAEDAE的大小。的大小。EEDDCCBBAAEEDDCCBBAA跃一跃跃一跃解:∵∠BAC=88°,AE是△ABC的角平分线∴∠BAE=∠DAC=∠BAC=44°又∵AD是△ABC的高∴∠ADB=90°又∵∠B=55°∴∠BAD=180°-∠B-∠ADB=180°-55°-90°=35°故∠DAE=∠BAE-∠BAD=44°-35°=9°½这节课你有那些收获?有哪些困惑?