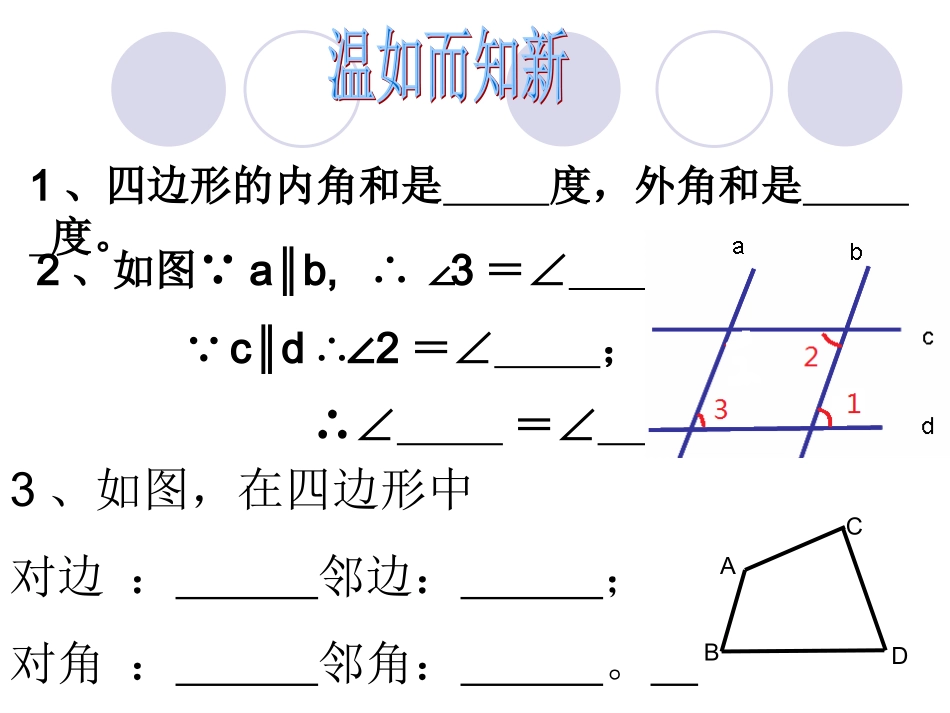
人教版八年级下册工作单位:台山市育英中学授课人:陈羡礼1、四边形的内角和是度,外角和是度。2、如图∵ab,∥∴∠3=∠;∵cd∥∴∠2=∠;∴∠=∠。ABCD3、如图,在四边形中对边:邻边:;对角:邻角:。观察这些图片,它们是否都有平行四边形的形象?观察抽象形成概念你还记得平行四边形的定义吗?两组对边分别平行的四边形叫做平行四边形.1.平行四边形定义:有两组对边分别平行的四边形叫做平行四边形.2、符号:表示平行四边形“□”ABDC3、记作:4、读作:5、几何语言:∴四边形ABCD是平行四边形平行四边形ABCD□ABCD∵AB∥CD,AD∥BC∵四边形ABCD是平行四边形∴AB∥CD,AD∥BC判断一个四边形是否为平行四边形一个平行四边形具有的性质对于平行四边形,从定义出发,你能得出它的其它的性质吗?概括证明探究性质给出图形定义→研究图形性质→探索图形判定条件回忆我们的学习经历,研究几何图形的一般思路是什么?猜想:平行四边形对角相等,对边相等.把平行四边形沿着对角线剪开,看看对边、对角有什么关系?ABDC性质1:平行四边形的对边相等.性质2:平行四边形的对角相等.ABDC性质1:平行四边形的对边相等.几何语言:∵四边形ABCD是平行四边形∴AB=CD,AD=BC性质2:平行四边形的对角相等.几何语言:∵四边形ABCD是平行四边形∴∠A=∠C,∠B=∠D性质3:平行四边形的邻角互补。几何语言:∵四边形ABCD是平行四边形∴∠A+∠B=1800,∠B+∠D=18001.1.平行四边形的平行四边形的对边平行且相等对边平行且相等平行四边形的性质:2.2.平行四边形的平行四边形的对角相等.对角相等.已知:ABCD(如图)求证:AB=CD,BC=DA;∠B=D∠,∠BAD=DCB∠即∠BAD=∠DCB证明:连结AC∵ABCD∥,ADBC∥(平行四边形的对边平行)∴∠1=∠2,∠3=∠4∠1=∠2,AC=CA,∠3=∠4∴ABCCDA≌(ASA)∴AB=CD,BC=DA,∠B=∠D又∵∠1=∠2,∠3=∠4∴∠1+∠4=∠2+∠3在ABC和CDA中ABCD1234概括证明探究性质归纳:(1)有关四边形的问题常常转化为三角形问题解决;(2)平行四边形的一条对角线把平行四边形分成两个全等的三角形;ABCD1、如图:在ABCD中,根据已知你能得到哪些结论?为什么?32cm30cm32cm30cmABCD56°56°124°124°小试牛刀:例题教学:例题教学:例1如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少?解:∵四边形ABCD是平行四边形BCAD;CDAB)m(8CD36ADCDBCAB又)m(10BCAD∵AB=8随堂练习:AADDBBCC401.在ABCD中,AD=40,CD=30,∠B=60°,则BC=;AB=;∠A=,C=,D=∠∠30120°120°60°2.在ABCD中,∠ADC=120°,∠CAD=20°,则∠ABC=,∠CAB=120°40°例1如图在ABCD中,AEBC,CFAD,⊥⊥垂足分别为E,F。求证:BE=DFAADDBBCCEF例题:HABCDG若a//b,作AD//GH//BC,分别交b于D、H、C,交a于A、G、B.两条平行线间的距离则GH=AD=BC.两条平行线之间的平行线段相等则DAHGCB.(应用性质1)若a//b,DA、GH、CB垂直于a,交a于A、G、B,交b于D、H、C.baABCDabHG点到直线的距离==相等应用知识解决问题例3△ABC是等腰三角形,AB=AC,P是底边BC上一动点,PE∥AB,PF∥AC,点E,F分别在AC,AB上.求证:PE+PF=AB.ABCEFP小结:1.概念:四边形两组对边平行四边形分别平行2.性质:性质一:对边平行,相等性质二:对角相等,邻角互补3.两平行线的距离相等4、平行四边形的周长:;平行四边形的面积:。作业:教科书习题18.1第1,2题,选做7,8题.课后作业