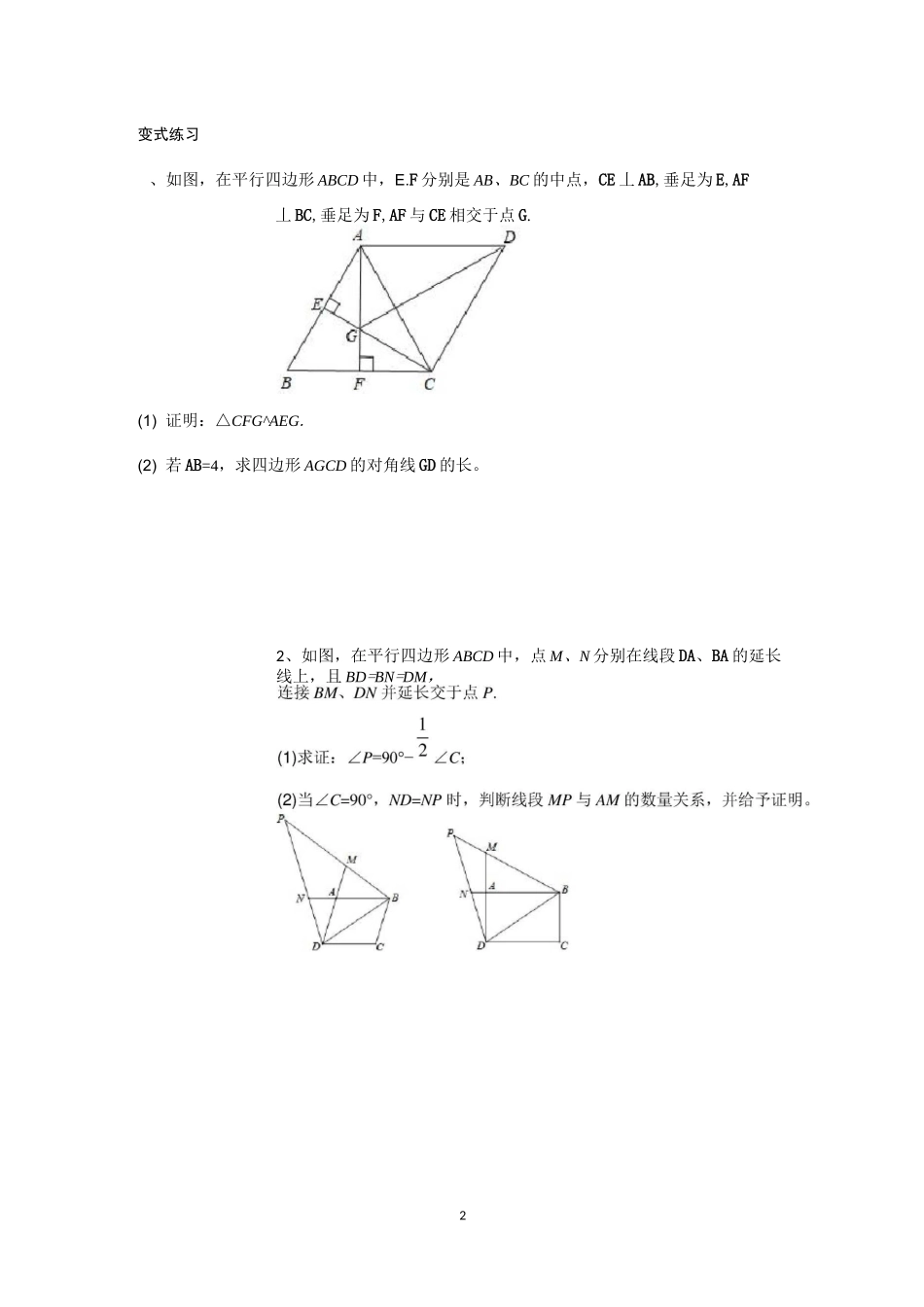
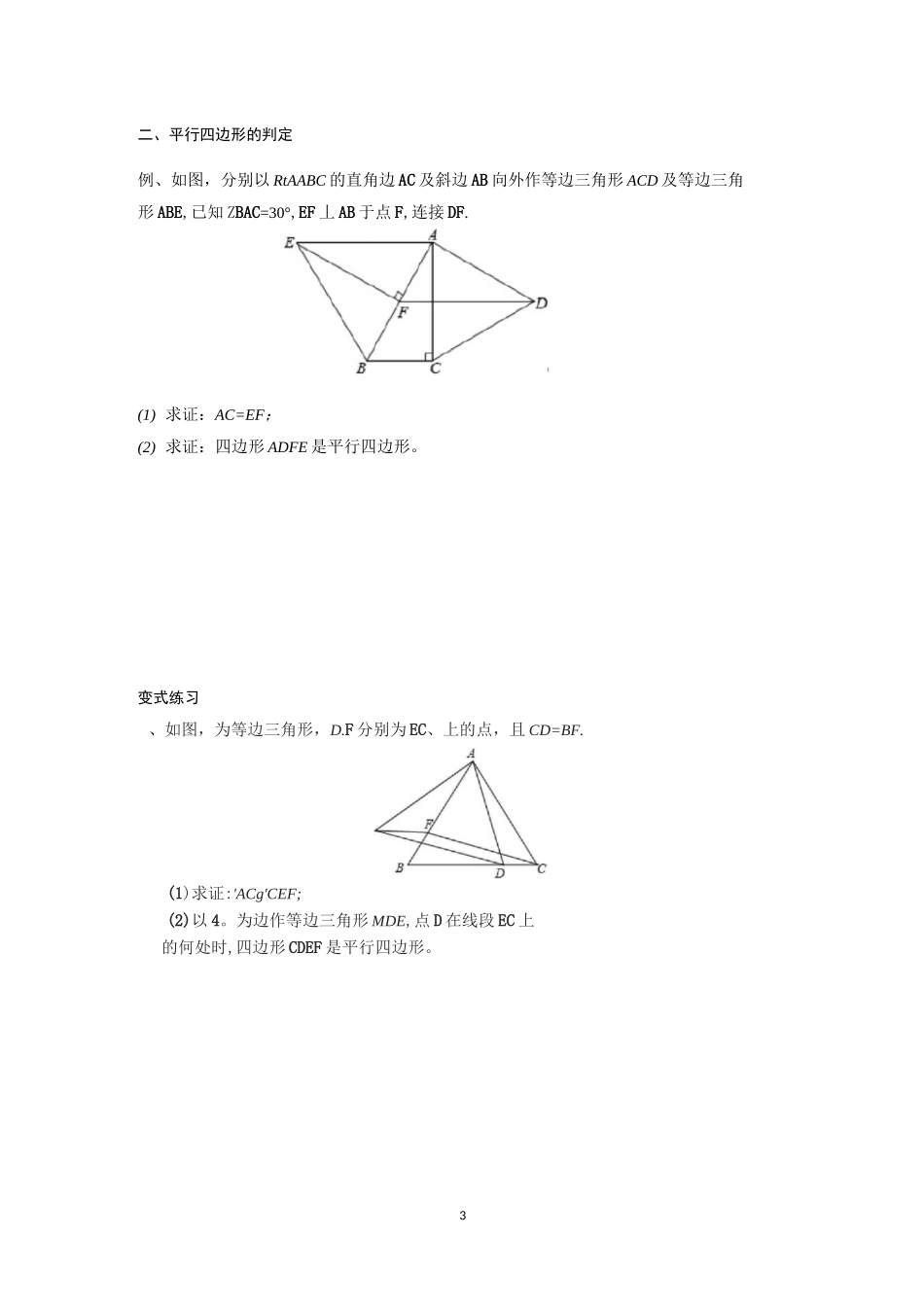
1平行四边形与特殊平行四边形(专题与提升)一、平行四边形的性质例、如图,在口ABCD中,各内角的平分线分别相交于点E,F,G,H.(1)求证:△ABG^^CDE;(2猜一猜:四边形EFGH是什么样的特殊四边形?证明你的猜想;(3)若AB=6,BC=4,ZDAB=60°,求四边形EFGH的面积。2变式练习、如图,在平行四边形ABCD中,E.F分别是AB、BC的中点,CE丄AB,垂足为E,AF丄BC,垂足为F,AF与CE相交于点G.(1)证明:△CFG^AEG.(2)若AB=4,求四边形AGCD的对角线GD的长。2、如图,在平行四边形ABCD中,点M、N分别在线段DA、BA的延长线上,且BD=BN=DM,3二、平行四边形的判定例、如图,分别以RtAABC的直角边AC及斜边AB向外作等边三角形ACD及等边三角形ABE,已知ZBAC=30°,EF丄AB于点F,连接DF.(1)求证:AC=EF;(2)求证:四边形ADFE是平行四边形。变式练习、如图,为等边三角形,D.F分别为EC、上的点,且CD=BF.(1)求证:'ACg'CEF;(2)以4。为边作等边三角形MDE,点D在线段EC上的何处时,四边形CDEF是平行四边形。4、如图,在平面直角坐标系xOy,直线y=x+l与y=-2x+4交于点A,两直线与x轴分别交于点B和点C,D是直线AC上的一个动点,直线AB上是否存在点E,使得以E,D,O,A为顶点的四边形是平行四边形?若存在,求出点E的坐标;若不存在,请说明理由。三、三角形中位线定理例、⑴如图1,在四边形ABCD中,AB=CD,E,F分别是AD,BC的中点,连接FE并延长,分别与BA,CD的延长线交于点M,N.求证:/BME=/CNE;(提示:取BD的中点H,连接FH,HE作辅助线)(2)如图2,在△ABC中,F是BC边的中点,D是AC边上一点,E是AD的中点,直线FE交BA的延长线于点G,若AB=DC=2,ZFEC=45°,求FE的长度。5变式练习、⑴回顾定理:如图1,在△ABC中,DE是△ABC的中位线。那么DE与BC的关系有(2)运用定理:如图2,在四边形ABCD中,ZABC=50°,ZBCD=40。,点F为AC的中点,点6、在△ABC中,AC=BC,ZACB=90°,点D为AC的中点。(1)如图1,E为线段DC上任意一点,将线段DE绕点D逆时针旋转90°得到线段DF,连接CF,过点F作FH丄FC,交直线AB于点H.判断FH与FC的数量关系并加以证明;(2)如图2,若E为线段DC的延长线上任意一点,(1)中的其他条件不变,你在⑴中得出的结论是否发生改变,直接写出你的结论,不必证明。7四、菱形的性质例、在菱形ABCD中,P是直线BD上一点,点E在射线AD上,连接PC.⑴如图1,当ZBAD=90°时,连接PE,交CD与点F,若ZCPE=90°,求证:PC=PE;(2如图2,当ZBAD=60°时,连接PE,交CD与点F,若ZCPE=60°,设AC=CE=4,求BP的长。8变式练习、如图,在菱形ABCD中,ZBAD=60°,M为对角线BD延长线上一点,连接AM和CM,E为CM上一点,且满足CB=CE,连接BE,交CD于点F.⑴若ZAMB=30°,且DM=3,求BE的长;(2)证明:AM=CF+DM.9、如图1已知ABCD是菱形,AEFP的顶点E,F,P分别在线段AB,AD,AC上,且EP=FP.(1)证明:ZEPF+ZBAD=180。;(2)如图2,若ZBAD=120°,证明:AE+AF=AP.10、如图,在边长为4的菱形ABCD中,BD=4,E.F分别是边AD、CD上的动点,且AE+CF=4,连接BE、EF、FB.DB(1)证明:BE=BF(2)求ABEF面积的最小值。11五、菱形的判定例、已知:如图,口ABCD的两条对角线相交于点O,E是BO的中点。过点B作AC的平行线BF,交CE的延长线于点F,连接AF.BC(1)求证:△FBE兰NCOE;(2)将_ABCD添加一个条件,使四边形AFBO是菱形,并说明理由。12变式练习、如图1,在AABC和AEDC中,AC=CE=CB=CD;ZACB=ZDCE=90°,AB与CE交于F,ED与AB,BC,分别交于M,H.(1)求证:CF=CH;(2)如图2,△ABC不动,将AEDC绕点C旋转到ZBCE=45°时,试判断四边形ACDM是什么四边形?并证明你的结论。B2、Rt^ABC与Rt^FED是两块全等的含30。、60°角的三角板,按如图(一)所示拼在一起,CB与DE重合。⑴求证:四边形ABFC为平行四边形;(2)取BC中点O将△ABC绕点O顺时钟方向旋转到如图(二)中△ABC,位置,直线BC与AB、CF分别相交于P、Q两点,猜想OQ、OP长度的大小关系,并证明你的猜想;(3)在(2)的条件下,指出当旋转角至少为多少度时,四边形PCQB为菱形?(不要求证明)A13六、矩形的性质例、在矩形ABCD中,AB=CD=10cm、BC=AD=8cm,动点P从A点出发沿AnBnCnD路线运动到D停止;动点Q从D出发,沿D^C^B^A路线运动到A停止;若P、Q同时出发,点P速度为1cmS点Q速度为2cmS,6s后P、Q...