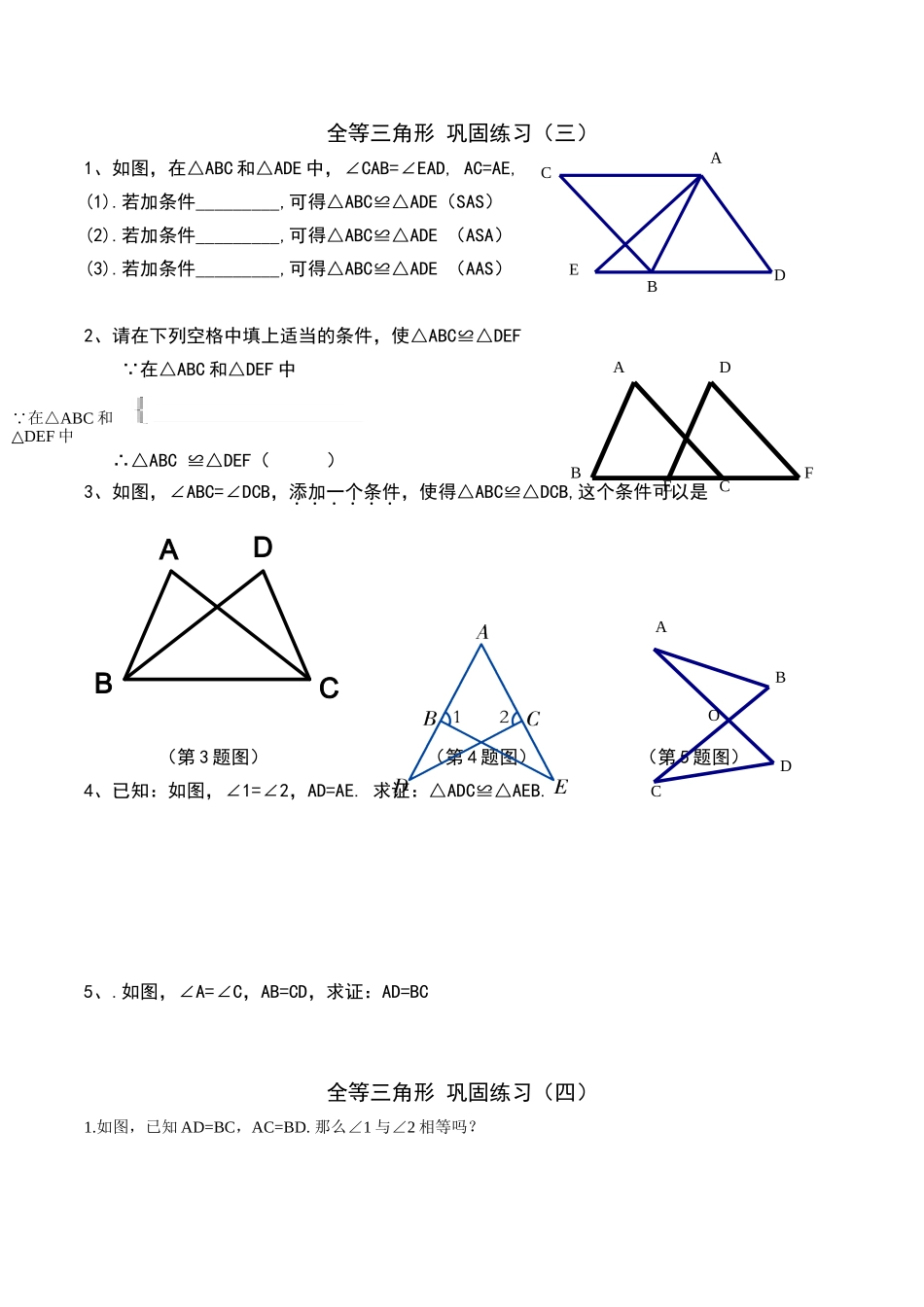
全等三角形巩固练习(三)1、如图,在△ABC和△ADE中,∠CAB=∠EAD,AC=AE,(1).若加条件_________,可得△ABC≌△ADE(SAS)(2).若加条件_________,可得△ABC≌△ADE(ASA)(3).若加条件_________,可得△ABC≌△ADE(AAS)2、请在下列空格中填上适当的条件,使△ABC≌△DEF∵在△ABC和△DEF中∴△ABC≌△DEF()3、如图,∠ABC=∠DCB,添加一个条件,使得△ABC≌△DCB,这个条件可以是DCBA(第3题图)(第4题图)(第5题图)4、已知:如图,∠1=∠2,AD=AE.求证:△ADC≌△AEB.5、.如图,∠A=∠C,AB=CD,求证:AD=BC全等三角形巩固练习(四)1.如图,已知AD=BC,AC=BD.那么∠1与∠2相等吗?ABCDE∵在△ABC和DEF△中ABCDEFABCDO2.如图,点A,C,B,D在同一条直线上,AC=BD,AE=CF,BE=DF.求证:AE∥CF,BE∥DF.3.如图,已知AB=CD,BC=DA。你能说明△ABC与△CDA全等吗?你能说明AB∥CD,AD∥BC吗?为什么?4、如图,AB=AC,BD=CD,BH=CH,图中有组全等的三角形,请分别写出这几组全等的三角形,并写明判定的方法全等三角形综合性练习一、知识点回顾1、全等三角形有哪些性质:①__________;②___________.2、判断全等三角形的方法有:①_______;②________;③________;④_________;3、如何找判定三角形全等的条件?①__________;②___________.4、书写证明过程注意的问题:DBACHDCBA(1)要写出在哪两个三角形中;(2)要按定理的顺序摆出三个条件,(注意边、角的对应关系)用大括号括起来;(3)写出结论。(书写时,要注意字母的对应关系。)5、通过判定三角形全等能解决哪些问题?证明线段(或角相等)转化成证明线段(或角)所在的两个三角形全等二、巩固性练习1、如图,AC=BD,AB=DC,求证:∠B=∠C2、如图AB=AC,BD=CD,求证:∠B=∠C.3、如图,CE⊥AB于E,BD⊥AC于D,BD、CE交于点O,且OD=OE,求证:AB=AC.4、如图,AB=AE,∠B=∠E,∠BAC=∠EAD,∠CAF=∠DAF,求证:AF⊥CD.5、如图,AB=AD,CD=CB,∠A+∠C=180°,试探索CB与AB的位置关系.ABCDEADCBABCDEOABCDEFABCD6、如图,AC=AB,BD=CD,AD与BC相交于O,求证:AD⊥BC.7、已知E是AD上的一点,AB=AC,AE=BD,CE=BD+DE,求证:∠B=∠CAD.8、在△ABC中,AB=AC,在AB上取一点D,在AC的延长线上取一点E,使BD=CE,连结DE交BC于F,求证:DF=EF.9、在△ABC中,AB=AC,在AB上取一点D,在AC的延长线上取一点E,连结DE交BC于F,若DF=EF,求证:BD=CE.ABCDOABCDEABCDEF10、已知∠1=∠2,∠3=∠4,问AC=AD吗?说明理由。11、已知ED⊥AB,EF⊥BC,BD=EF,问BM=ME吗?说明理由。12、在△ABC中,高AD与BE相交于点H,且AD=BD,则△BHD≌△ACD,为什么?13、已知AC=AB,AE=AD,∠1=∠2,问∠3=∠4吗?ABCDEFABCD1234ABCDEFMABCDEH1234ABCDE14.已知∠1=∠2,BC=AD,求证:AC=BD15、已知AD=AE,BD=CE,求证:△ABC是等腰三角形。16、已知∠1=∠2,AC=BD,E,F,A,B在同一直线上,求证:∠3=∠417、已知:如图,∠A=∠D=90°,AC,BD交于O,AC=BD,求证:OB=OC.12ABCDO12ABCDE1234ABCDEFABCDO