四边形考点透视VIP免费

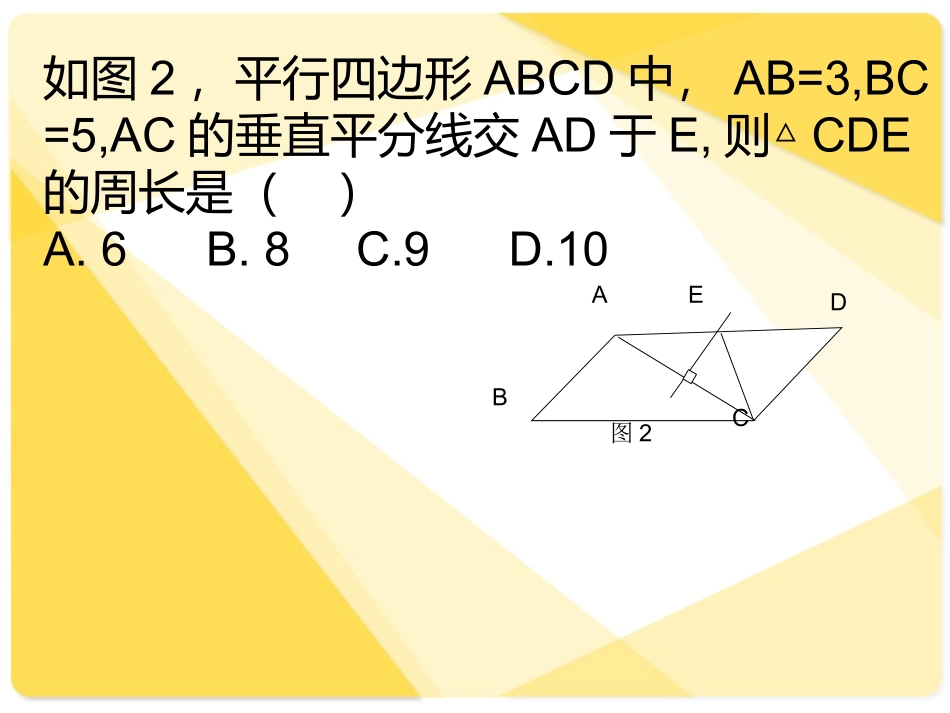
例1：如图1，DBAC∥，DB=AC，E是AC的中点.求证：BC=DE.证明： E为AC中点，∴EC=AC. DB=AC，∴EC=DB. DBAC∥，∴四边形BECD为平行四边形,BC=DE.∴图1DECBA2121如图2，平行四边形ABCD中，AB=3,BC=5,AC的垂直平分线交AD于E,则△CDE的周长是（）A.6B.8C.9D.10图2DCBAE如图3，已知长方形ABCD，过点C引∠A的平分线AM的垂线，垂足为M，AM交BC于E，连结MB、MD。（1）求证：BE=DC；（2）求证：∠MBE=MDC∠µÚ19ÌâͼMEDCBA图3证明:(1) 四边形ABCD是矩形,AB=C∴D,ABC=BAD=.∠∠ AM平分∠BAD,BAE=BAD=45∴∠∠0,∴△ABE为等腰直角三角形,AB=BE,BE∴∴=DC.(2)ABE △为等腰直角三角形,AEB=45∴∠0,BEM=135∴∠0,MEC=45∠0.AMCM, ⊥∴△MEC为等腰直角三角形,MC=ME,MCE∴∠=450.MCD=135∴∠0.MEBMCD,M∴△≌△∴∠BE=MDC.∠09021在正方形ABCD中，点P是CD上一动点，连结PA，分别过点B、D作BEPA⊥、DFPA⊥，垂足为E、F，如图①．（1）请探究BE、DF、EF这三条线段长度具有怎样的数量关系．若点P在DC的延长线上（如图②），那么这三条线段的长度之间又具有怎样的数量关系？若点P在CD的延长线上呢（如图③）？请分别直接写出结论；（2）请在（1）中的三个结论中选择一个加以证明(1)图①的结论是BE=EF+DF;图②的结论是DF=BE+EF;图⒀的结论是EF=BE+DF;(2)证明图① DFPA,DAF+ADF=90⊥∴∠∠0.DAF+BA ∠∠E=900,ADF=BAE.∴∠∠ BEPA,AEB=AFD=90⊥∴∠∠0.在正方形ABCD中,AB=AD,∴△ABE≌△DAF,BE=AF,AE=DF.AF=AE+EF,BE=DF+EF.∴ ∴证明： EF垂直平分AC，∴EF⊥AC，且AO＝CO. 四边形ABCD是平行四边形,∴AE∥FC,∴∠EAO=∠FCO.[来源:学科网]∴△AOE≌△COF,∴AE=CF.∴四边形AECF是平行四边形.又 AC⊥EF,∴平行四边形AECF是菱形.例题赏析⒊在正方形ABCD中，对角线AC、BD相交于点O，点Q是CD上任意一点，DP⊥AQ交BC于点P．⑴求证：DQ=CP；PODABCQ⑵OP与OQ有何关系？试证明你的结论．4MABCDADPBCPEMCPFMBEFABCDPEMF、如图，点是矩形的边的中点，点是边上的一动点，，，垂足分别为、。当矩形的长和宽满足什么条件时，四边形为矩形？猜想并说明理由。ABCDEPEFM变一变如图所示，正方形ABCD中，P为BD上一点，PEBC⊥于E，PFDC⊥于F。试说明：AP=EFABCDPEF解:连接PC PEBC⊥，PFDC⊥而四边形ABCD是正方形∴∠FCE=90°∴四边形PECF是矩形∴PC=EF又 四边形BAPC是以BD为轴的轴对称图形∴AP=PC∴AP=EF如图,以△ABC的边AB、AC向形外作正方形ABDE和ACFG，M是BC的中点．求证：⑴CE=BG；⑵EG=2AM．HMEDFGBCA例题赏析4.在正方形ABCD中,AC是对角线,AE平分∠BAC,试猜想AB、AC、BE之间的关系，并证明你的猜想．GFEDABC25，如图20，已知正方形ABCD的对角线AC、BD相交于点O，E是AC上一点，连结EB，过点A作AMBE⊥，垂足为M，AM交BD于点F.(1)试说明OE＝OF；(2)如图21，若点E在AC的延长线上，AMB⊥E于点M，交DB的延长线于点F，其它条件不变，则结论“OE＝OF”还成立吗?如果成立，请给出说明理由；如果不成立，请说明理由.图20EMFCODBAO图21EFOCMDAB(1) 四边形ABCD是正方形，∴∠BOE=AOF∠＝90°，OB＝OA，又 AM⊥BE，∴MEA+MAE＝90°=AFO+MAE，∴MEA＝AFO，∴RtBOE△可以看成是绕点O旋转90°后与RtAOF△重合，∴OE=OF；(2)OE＝OF成立.证明： 四边形ABCD是正方形，∴∠BOE=AOF∠＝90°，OB＝OA又 AM⊥BE，∴∠F+MBF∠＝90°＝∠B+OBE∠，又 ∠MBF＝∠OBE，∴∠F＝∠E，所以RtBOE△可以看成是由RtAOF△绕点O旋转90°以后得到的，∴OE=OF；24．（10分）如图11，在矩形ABCD中，AB＝6，BC＝8．将矩形ABCD沿CE折叠后，使点D恰好落在对角线AC上的点F处．（1）求EF的长；（2）求梯形ABCE的面积。设EF＝x．依题意知：△CDE≌△CFE．∴DE＝EF＝x，CF＝CD＝6,在中，有RtAEFAEAFEF222即()84222xx∴x3即EF＝3．由（1）知：AE＝8－3＝5,∴·梯形SAEBCABABCE()()2586239如图，O是矩形ABCD的对角线的交点，DE∥AC，CEBD∥，DE和CE相交于E，求证：四边形OCED是菱形。证明： DEAC,CEB∥∥D□∴OCED 矩形ABCD∴AC=BD,AO=CO,BO=DO∴OC=OD∴四边形OCED是菱形。已知：正方形...