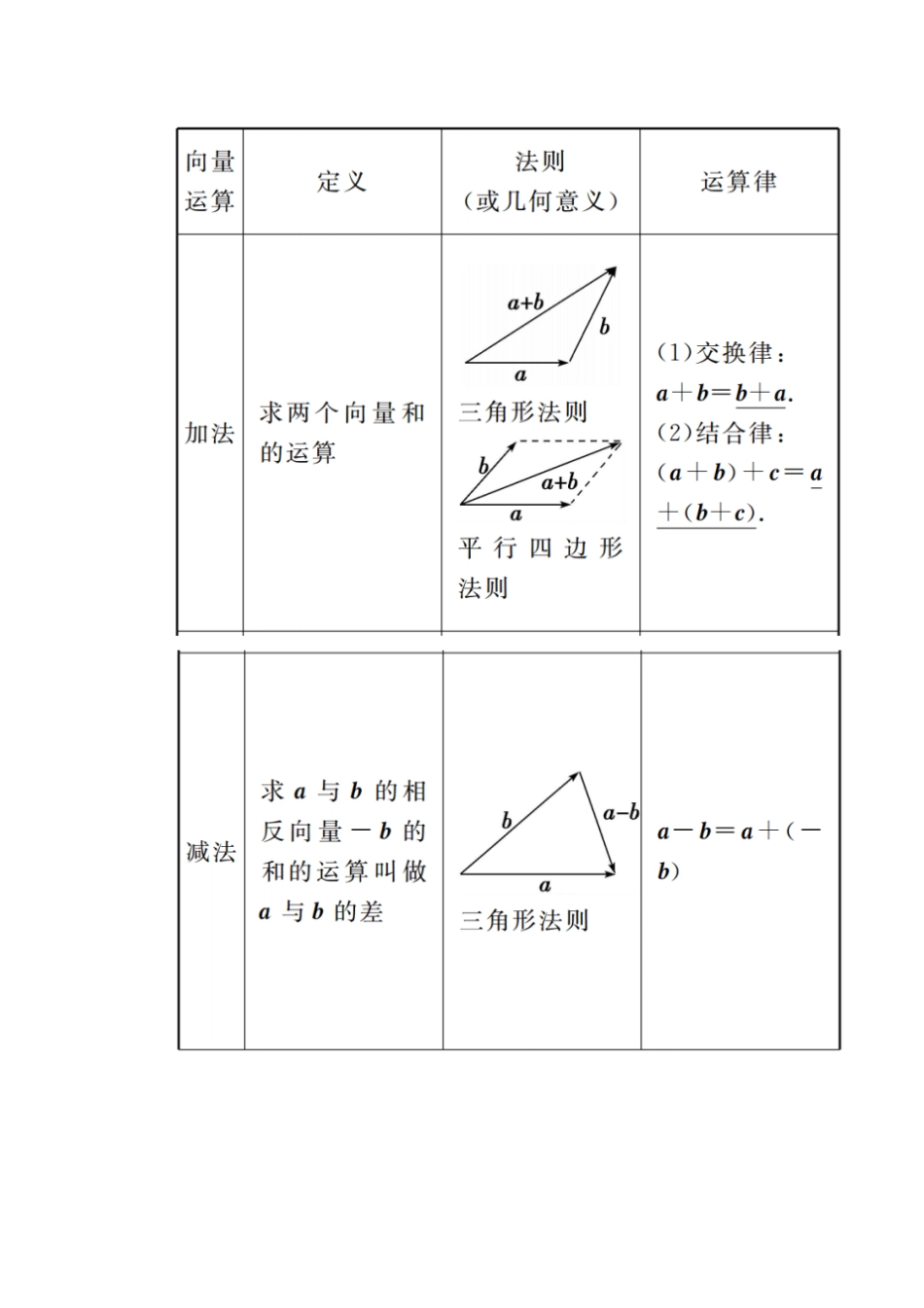
第一节平面向量的基本概念及线性运算【最新考纲】1.了解向量的实际背景,理解平面向量的概念和两个向量相等的含义,理解向量的几何表示.2.掌握向量加法、减法的运算,理解其几何意义.3.掌握向量数乘的运算及其几何意义,理解两个向量共线的含义.4.了解向量线性运算的性质及其几何意义.1.向量的有关概念(1)向量:既有大小又有方向的量叫做向量,向量的大小叫做向量的长度(或模).(2)零向量:长度为0的向量,其方向是任意的.(3)单位向量:长度等于1个单位的向量.(4)平行向量:方向相同或相反的非零向量.平行向量又叫共线向量.规定:0与任一向量平行.(5)相等向量:长度相等且方向相同的向量.(6)相反向量:长度相等且方向相反的向量.2.向量的线性运算3.共线向量定理向量ɑ(ɑ≠0)与b共线的充要条件是存在唯一一个实数λ,使得b=λɑ.1.(质疑夯基)判断下列结论的正误.(正确的打“√”,错误的打“×”)(1)向量与有向线段是一样的,因此可以用有向线段来表示向量.()(2)若ɑ∥b,b∥c,则ɑ∥c.()(3)ɑ∥b是ɑ=λb(λ∈R)的充要条件.()(4)△ABC中,D是BC的中点,则AD→=12(AC→+AB→).()答案:(1)×(2)×(3)×(4)√2.D是△ABC的边AB上的中点,则向量CD→等于()A.-BC→+12BA→B.-BC→-12BA→C.BC→-12BA→D.BC→+12BA→解析: D是△ABC的边AB上的中点,∴CD→=CB→+12BA→=-BC→+12BA→.答案:A3.(2014·课标全国Ⅰ卷)设D,E,F分别为△ABC的三边BC,CA,AB的中点,则EB→+FC→=()A.AD→B.12AD→C.BC→D.12BC→解析:由于D,E,F分别是BC,CA,AB的中点,所以EB→+FC→=-12(BA→+BC→)-12(CA→+CB→)=-12(BA→+CA→)=12(AB→+AC→)=12×2AD→=AD→.答案:A4.如右图,已知D,E,F分别是△ABC的边BC,AB,AC的中点,则下列说法正确的是()A.AE→=AF→B.EF→=CD→C.EF→=BD→D.DB→=DC→解析: 向量EF→与向量BD→方向相同,且模相等,∴EF→=BD→.答案:C5.(2015·课标全国Ⅱ卷)设向量ɑ,b不平行,向量λɑ+b与ɑ+2b平行,则实数λ=________.解析: λɑ+b与ɑ+2b平行,∴λɑ+b=t(ɑ+2b),则λɑ+b=tɑ+2tb,∴λ=t,1=2t.解得λ=t=12.答案:12一条规律一般地,首尾顺次相接的多个向量的和等于从第一个向量起点指向最后一个向量终点的向量.三个结论1.若P为线段AB的中点,O为平面内任一点,则OP→=12(OA→+OB→).2.OA→=λOB→+μOC→(λ,μ为实数),若点A,B,C共线,则λ+μ=1.3.若A,B,C是平面内不共线的三点,则PA→+PB→+PC→=0?P为△ABC的重心.三个防范1.向量共线的充要条件中要注意“ɑ≠0”,否则λ可能不存在,也可能有无数个.2.进行向量减法运算时,一定将向量平移至同一起点.3.证明三点共线问题,可用向量共线来解决,但应注意向量共线与三点共线的区别与联系,当两向量共线且有公共点时,才能得出三点共线.一、选择题1.把平面上所有的单位向量平移到相同的起点上,那么它们的终点所构成的图形是()A.一条线段B.一段圆弧C.两个孤立点D.一个圆解析:由单位向量的定义可知,如果把平面上所有的单位向量平移到相同的起点上,则所有的终点到这个起点的距离都等于1,所有的终点构成的图形是一个圆.答案:D2.设ɑ、b都是非零向量,下列四个条件中,使ɑ|ɑ|=b|b|成立的充分条件是()A.ɑ=-bB.ɑ∥bC.ɑ=2bD.ɑ∥b且|ɑ|=|b|解析:ɑ|ɑ|表示与ɑ同向的单位向量,b|b|表示与b同向的单位向量,只要ɑ与b同向,就有ɑ|ɑ|=b|b|,观察选项易知C满足题意.答案:C3.(2015·佛山一中期中考试)如下图,一直线EF与平行四边形ABCD的两边AB、AD分别交于E、F两点,且交其对角线AC于K,其中,AE→=25AB→,AF→=12AD→,AK→=λAC→,则λ的值为()A.29B.27C.25D.23解析: AE→=25AB→,AF→=12AD→,则AB→=52AE→,AD→=2AF→, AC→=AB→+AD→,∴AK→=λAC→=λ(AB→+AD→)=λ52AE→+2AF→=52λAE→+2λAF→,由E,F,K三点共线可得,52λ+2λ=1,解得λ=29.答案:A4.设P是△ABC所在平面内的一点,BC→+BA→=2BP→,则()A.PA→+PB→=0B.PB→+PC...