对数运算练习题VIP免费

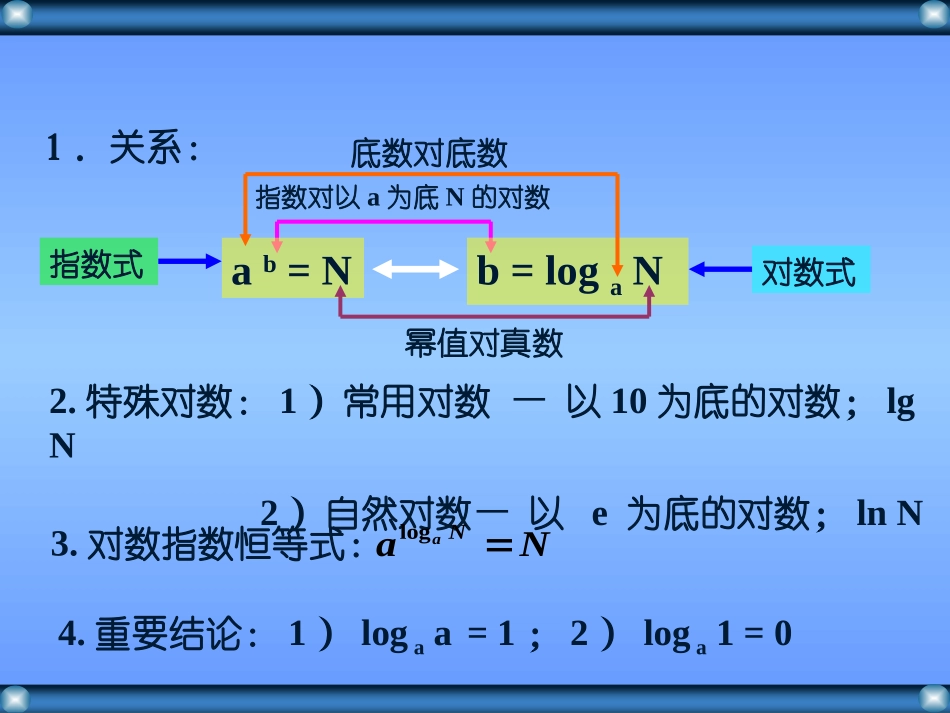
对数的运算指数对以a为底N的对数ab=Nb=logaN指数式对数式底数对底数幂值对真数１．关系：2.特殊对数：1）常用对数—以10为底的对数；lgN2）自然对数—以e为底的对数；lnN3.对数指数恒等式：NaNalog4.重要结论：1）logaa=1；2）loga1=0复习上节内容2.2.对数的性质对数的性质(1)(1)负数和零没有对数；负数和零没有对数；(2)1(2)1的对数是零的对数是零,,即即loglogaa1=01=0；；(3)(3)底的对数等于底的对数等于1,1,即即loglogaaaa=1=1010logNaaNaNa，且3.对数恒等式1.1.对数一般地对数一般地,,如果如果aaxx=N(=N(aa＞＞0,0,aa≠1),≠1),那么那么数数xx叫做以叫做以aa为底为底NN的对数的对数,,记作记作loglogaaN=N=xx,,其其中中aa叫做对数的底数叫做对数的底数,N,N叫做真数叫做真数,,式子式子loglogaaNN叫做对数式叫做对数式..常用对数常用对数NN的常用对数的常用对数log10N,log10N,记作记作lgNlgN自然对数自然对数NN的自然对数的自然对数logeNlogeN简记作简记作lnN.lnN.新授内容：积、商、幂的对数运算法则：如果a>0，a1，M>0，N>0有：)4(Mlogn1Mlog)3(R)M(nnlogMlog)2(NlogMlogNMlog)1(NlogMlog(MN)loganaanaaaaaaa证明：①设,logpMa,logqNa由对数的定义可以得：,paMqaN∴MN=qpaaqpaqpMNalog即证得)1(NlogMlog(MN)logaaa正因数的积的对数等于同一底数各个因数的对数的和证明：②设,logpMa,logqNa由对数的定义可以得：,paMqaN∴qpaaqpaqpNMloga即证得NM)(2NlogMlogNMlogaaa两个正数的商的对数等于被乘数的对数减去除数的对数证明：③设,logpMa由对数的定义可以得：,paMnpnaMnpMlogna即证得)(3R)M(nnlogMlogana正数的幂的对数等于幂的底数的对数乘以幂指数)4(Mlogn1Mlogana正数的正的方根的对数等于被开方数的对数除以根指数.①简易语言表达：“积的对数=对数的和”…②有时逆向运用公式③真数的取值范围必须是),0(④对公式容易错误记忆，要特别注意：,loglog)(logNMMNaaaNMNMaaaloglog)(log分析运用转化的思想,先通过假设,将对数式化成指数式,并利用幂的运算性质进行恒等变形;然后再根据对数定义将指数式化成对数式.11025101010logloglog)(log)(log))((log5353222)(log)(log1021010210探索：把左右两列中一定相等的用线连起来NMaaloglogNMalognaMlog)(logMNaNMaaloglogMnalogNMaaloglog)log(NMNMaaloglog)log(NMnaM)(log例1计算)42(log)1(75227log)2(9讲解范例解:)42(log752522log724log522log1422log=5+14=19解:27log9333log23log23323讲解范例8log7log3log)3(732解:8log7og3log7327lg8lg3lg7lg2lg3lg2lg2lg32lg2lg3=3例2讲解范例解（1）解（2）用,logxa,logyazalog表示下列各式：32log)2(;(1)logzyxzxyaazxyzxyaaalog)(loglog3121232log)(loglogzyxzyxaaazyxaaalogloglog31212logloglogzyxaaazyxaaalog31log21log218lg7lg37lg214lg)1(例3计算：讲解范例解法一：18lg7lg37lg214lg18lg7lg)37lg(14lg218)37(714lg201lg)32lg(7lg37lg2)72lg(2)3lg22(lg7lg)3lg7(lg27lg2lg018lg7lg37lg214lg解法二：例3计算：讲解范例9lg243lg)2(3lg23lg525解：1023lg)10lg(32lg)3lg(2.1lg10lg38lg27lg)3(2213213253lg3lg9lg243lg)2(2.1lg10lg38lg27lg)3(12lg23lg)12lg23(lg2323练习（1）（4）（3）（2）1.求下列各式的值：15log5log332lg5lg31log3log553log6log2236log2)25lg()313(log5155log32log2110lg11log50133log12.用lgｘ，lgｙ，lgｚ表示下列各式：练习（1）（4）（3）（2）)lg(xyzzxy2lgzxy3lg＝lgｘ＋２lgｙ－lgｚ；zyx2lg＝lgｘ＋lgｙ＋lgｚ；＝lgｘ＋３lgｙ－21lgｚ；zyxlglg2lg21ylgxlg4lg3lg)y3x2lg()yxlg(.4已知例.yx的值求1、指数式与对数式：ab=Nb=logaN指数式对数式底数对底数幂值对真数指数对...