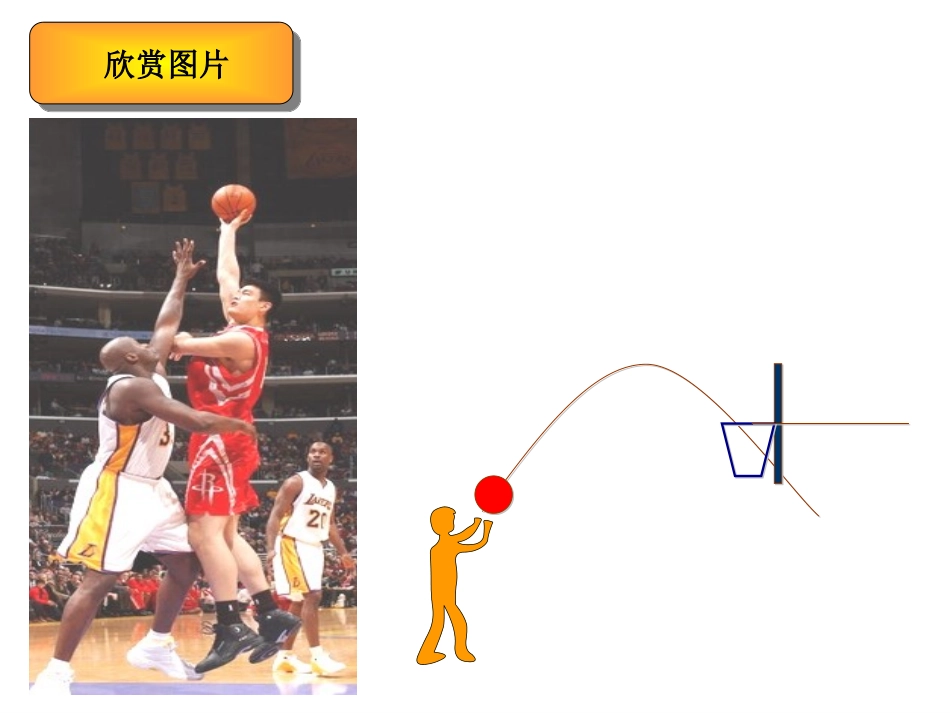
抛物线及其标准方程北师大版高中数学选修北师大版高中数学选修2-12-1安徽省太和中学姜翠翠欣赏图片欣赏图片动手做实验画抛物线.swf实验:如图,一块三角板的一条直角边紧靠直尺的边缘,取一条长为AC的绳子,一端固定在点A上,另一端固定在定点F上,把笔尖放在P点,AP紧靠三角板并把绳子绷紧,然后沿着直线l上下移动三角板作出点P移动的轨迹图形.Å×ÎïÏߵĶ¨Òå.gsp概念形成概念形成抛物线的定义:平面内与一个定点F和一条定直线(不过F)的距离相等的点的集合叫做抛物线。点F叫抛物线的焦点;直线叫做抛物线的准线。注意:(1)F不在l上;(2)若F在l上,轨迹为过F且与l垂直的直线.lll方程推导方程推导活动二:设抛物线的焦点F到准线的距离为p(p>0),即试求其方程。Flkl活动要求:1先独立思考,再小组讨论2组长汇总结果,黑板板书过程pPK=||标准方程··FMlN如何建立直角坐标系?想一想(1)(2)(3)FKMNFKMNFKMNxxxyyyooopxy22)2(22pxpy)2(22pxpy是抛物线的标准方程.焦点在x轴正半轴上,坐标是,准线方程为.)0(22>=ppxy)0,2(p2px巩固提高巩固提高小结:待定系数法求方程,先定形再定量,方程思想。例1:根据下列条件求抛物线的标准方程。(1)已知抛物线的的焦点坐标是F(2,0);(2)已知抛物线的准线方程是.活动三:23-x2(1)2(0).ypxp设抛物线的标准方程为解2,0.2,4,228.pppyx其焦点坐标为()根据题意有即因此标准方程为巩固提高巩固提高例2:点M与点F(4,0)的距离比它到直线l:x+6=0的距离小2,求点M的轨迹方程。小结:借助图形理解题意,巩固抛物线的定义,数形结合的思想。•1、一种圆锥曲线:抛物线的定义及其标准方程;•2、两个重要方法:定义法、待定系数法;•3、三种数学思想:数形结合、类比、方程的思想。总结升华总结升华(必做)1.课本第73页思考交流2.课本76页习题3-2,A组第5、6题.作业布置作业布置(选做)M是抛物线y2=2px(P>0)上一点,若点M的横坐标为x0,则点M到焦点的距离是