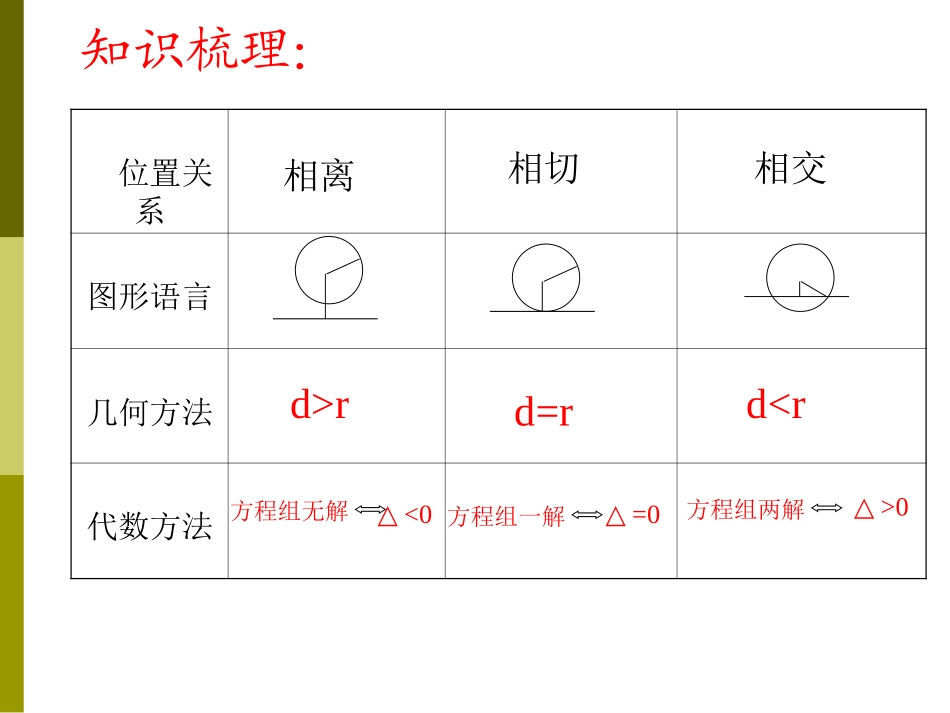
直线与圆的位置关系位置关系图形语言几何方法代数方法d>rd=rd0相离相交相切知识梳理:基础训练:3x+y-4=031、过点P(1,)与圆:x2+y2=4,相切的切线方程为.2、设直线2x+3y+1=0和圆x2+y2-2x-3=0相交于A、B两点,则弦AB的垂直平分线方程为____________.3、直线x+2y=0被圆x2+y2-6x-2y-15=0所截得的弦长等于.4、设M是圆(x-5)2+(y-3)2=9上的点,则点M到直线3x+4y-2=0的最短距离为________.0323yx254典型例题:例1已知圆C与y轴相切,圆心在直线l1:x-3y=0上,且在直线l2:y=x上截得的弦长为.求圆C的方程.72241xy分析4)1(22yx例2已知曲线与直线l:y=k(x-2)+4有两个不同的交点,则实数k的取值范围是.)1(yxyO12.例2已知曲线与直线l:y=k(x-2)+4有两个不同的交点,则实数k的取值范围是.241xy分析y=k(x-2)+4)1(4)1(22yyx过定点A(2,4)有两个不同的交点xy(2,1)C(-2,1)O.A(2,4)B241xy432214ACk125k分析y=k(x-2)+4)1(4)1(22yyx过定点A(2,4)有两个不同的交点圆心(0,1)直线kx-y+4-2k=0]43,125(k的取值范围是21322kkdxy(2,1)C(-2,1)O.A(2,4)B.例2已知曲线与直线l:y=k(x-2)+4有两个不同的交点,则实数k的取值范围是.变式1:若方程有两个不等实根,求k的取值范围.4)3(42xkx变式2:已知是圆上一动点,求下列各式的取值范围:(1);(2);(3);(4).),(yxpxy34xy22yxyx21)2()2(22yx解题回顾:在处理函数、方程、不等式等有关问题时,我们常借助于数形结合的思想方法来求解,可使较复杂问题变得更加直观、容易.在解析几何中更是如此.例3已知圆x2+y2-12x+32=0的圆心为Q,过点P(0,2)且斜率为k的直线与圆Q相交于不同的两点A,B.是否存在常数k,使得向量与共线?如果存在,求k的值;如果不存在,请说明理由.OBOAPQ巩固练习:1、已知圆C:(x-1)2+(y-2)2=25,直线l:(2m+1)x+(m+1)y-7m-4=0(mR∈),则直线l与圆C的位置关系是________.2、已知直线:ax+by+c=0(abc≠0)与圆:x2+y2=1相切,则三条边长分别为|a|、|b|、|c|的三角形的形状为__________.相交直角三角形一、判定直线和圆的位置关系的方法:1.比较d与r的大小2.判别式法二、在处理直线与圆相交,求弦长问题时,我们经常抓住半径、半弦、弦心距构成的直角三角形求解.在处理切线问题时,要抓住切线与过切点的半径垂直这个性质来解题.三、注意数形结合的思想的运用.小结: