5.3对数函数的图像和性质VIP免费

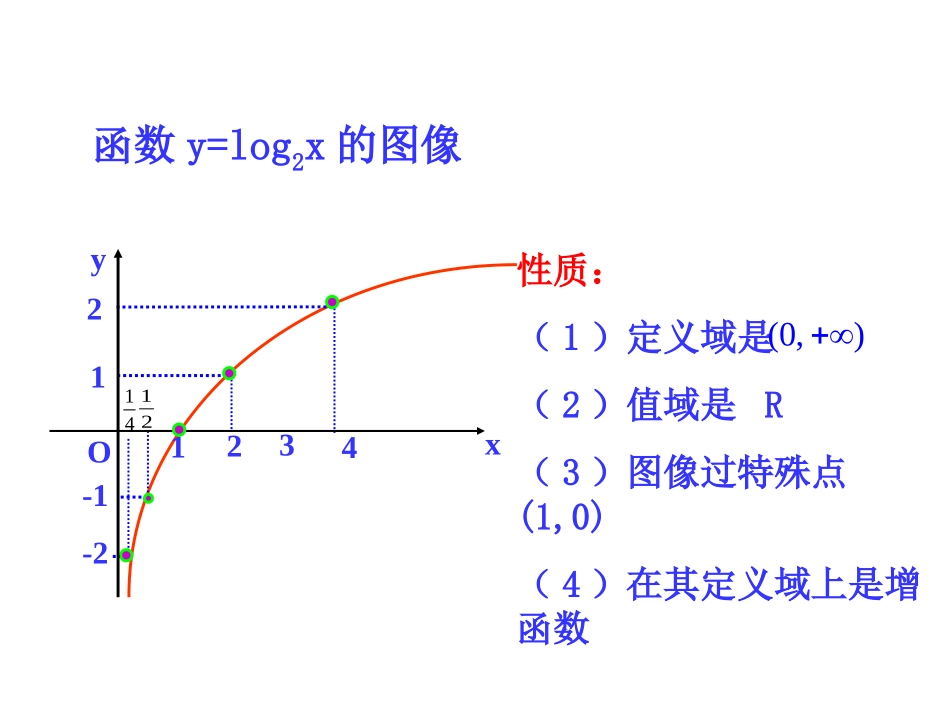
5.3对数函数的图像和性质1.对数函数的概念：我们把叫作对数函数，其中定义域是,值域是R,叫作对数函数的底数.aylogx(a0a1)且0,a2.指数函数和对数函数互为反函数.)1,0(logaaxyaxy=a21-1-2124Oyx32114性质：（1）定义域是（2）值域是R（3）图像过特殊点(1,0)（4）在其定义域上是增函数(0,)函数y=log2x的图像1.掌握对数函数的图像与性质.（重点）2.会应用对数函数的图像与性质解决一些简单问题.(难点）3.体会数形结合思想在研究函数问题中的应用.性质：（1）定义域是（2）值域是（3）图像过特殊点（4）在其定义域上是减函数21-1-2124Oyx32114(0,)R(1,0)对数函数y=log0.5x的图像0+∞+∞-∞(1,0)·xy(1,0)0yx增函数1.1a减函数1.01a1,0xy2.当时1,0xy当0时1,0xy2.当时1,0xy当0时+∞+∞-∞定义域（0，+∞）值域R过点（1，0),即1,0xy时logayx1a（）logayx01a（）减函数增函数单调性（1，0）过定点函数值变化情况值域（0，+∞）定义域图像函数R11oo)1(logaxya)10(logaxya1,0xy当时1,0xy当0时1,0xy当时1,0xy当0时归纳性质ⅠⅡⅣⅢ类比指数函数图像和性质的研究，研究对数函数的性质：思考：底数a是如何影响函数y=logax的?规律:在第一象限内，自左向右，图像对应的对数函数的底数逐渐变大.在直线x=1的右侧，当a>1时，底数越大，图像越接近x轴，当00,即x≠0，所以函数y=㏒ax2的定义域为{x|x≠0}.（2）因为4-x>0,即x<4，所以函数y=㏒a(4-x)的定义域为{x|x<4}.对数式有意义:底数大于0且不等于1,真数大于0.10.51log(3)(2)log(43).（）求下列函数的定义域：（）；xyxyx练一练：所以11，函数y=log2x是增函数，5.3>4.7,所以(2)因为0<0.2<1,函数y=log0.2x是减函数，7<9，所以log0.27>log0.2922log5.3log4.7(3)因为函数y=log3x是增函数，，所以,同理，所以π3>33logπlog31>=ππ1logπlog3=>3πlogπlog3>(4)当a>1时，函数y=logax在上是增函数，此时log3.1log5.2aa<当0),0（），（0【提升总结】利用对数函数的性质比较大小：当底数相同真数不同时，直接利用单调性即得结果；当底数不同真数相同时，可以根据对数函数图像与底数反映出来的规律比较大小；当真数与底数都不同时，常引入第三个数1或0，间接比较两个对数的大小.比较下列各组中两个值的大小：（1）55log9.4,log8.5（2）0.60.6log3.8,log2.7（3）2log5，3log5【变式练习】解：（1）函数5logyx在其定义域内是增函数，且9.48.5，所以55log9.4log8.5（2）函数0.6logyx在其定义域内是减函数，且3.82.7，所以0.60.6log3.8log2.7.(3)根据23loglogyxyx与的图像的位置关系可得2log53log5例3观察在同一坐标系内函数y=log2x(x∈（0，+∞）)与函数y=2x（x∈R）的图像，分析它们之间的关系.y=xyxQ(b,a)P(a,b)oy=2xy=xy=log2xP(a,b)Q(b,a)(1,0)(0,1)Oyx（1）（2）解：从图（1）上可以看出，点P（a,b）与点Q（b,a）关于直线y=x对称.函数y=log2x与函数y=2x互为反函数，对应于函数y=log2x图像上的任意一点P（a,b），P点关于直线y=x的对称点Q(b,a)总在函数y=2x图像上，所以，函数y=log2x的图像与函数y=2x的...