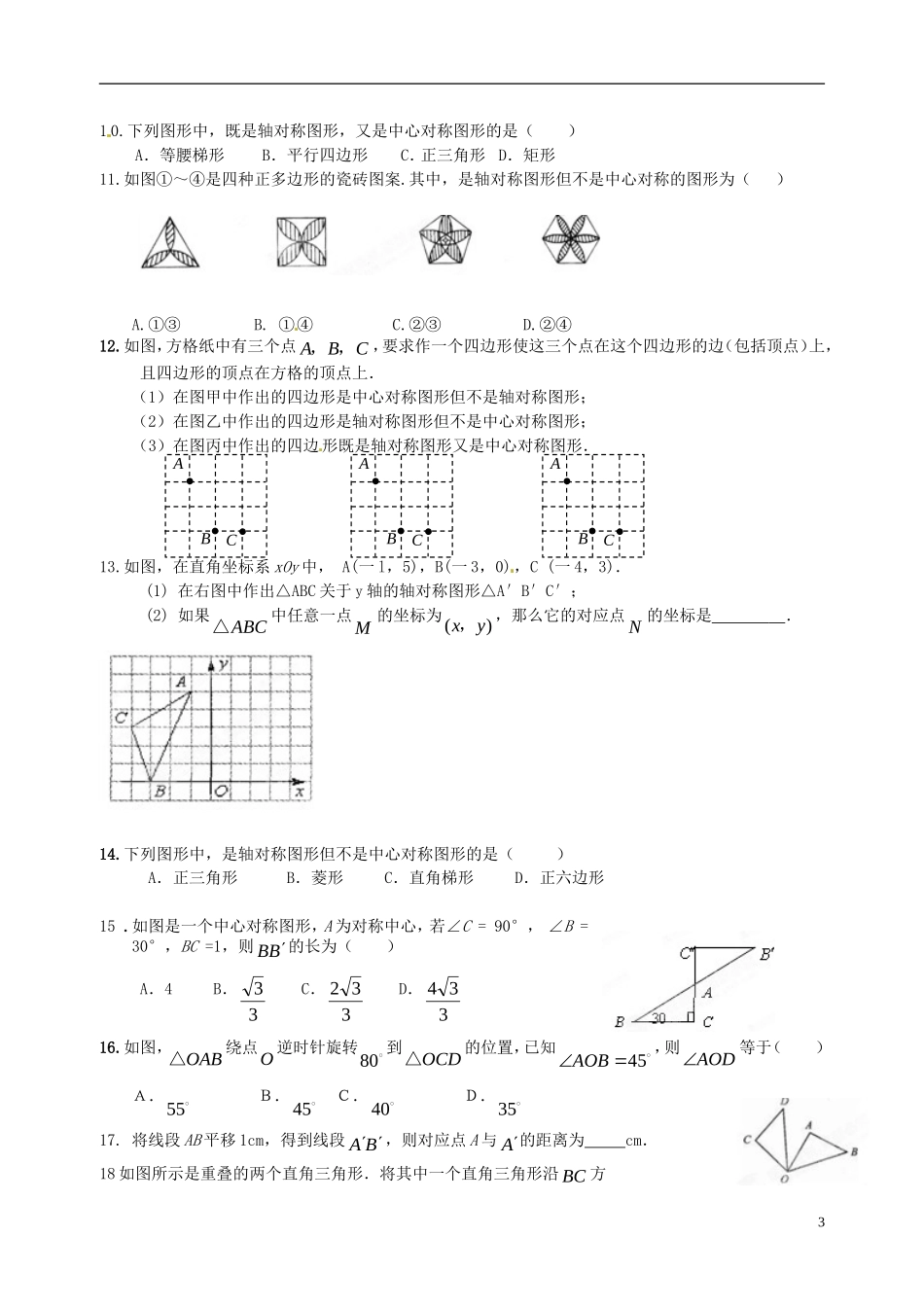
第17讲图形变换【知识点】一、视图与投影1.从观察物体时,看到的图叫做主视图;从观察物体时,看到的图叫做左视图;从观察物体时,看到的图叫做俯视图.2.主视图与俯视图的一致;主视图与左视图的一致;俯视图与左视图的一致.3.叫盲区.4.投影可分为平行投影与中心投影.其中所形成的投影叫平行投影;所形成的投影叫中心投影.5.利用光线是否平行或是否交于一点来判断是投影或投影,以及光源的位置和物体阴影的位置.二、平移1.一个图形沿着一定的方向平行移动一定的距离,这样的图形运动称为______,它是由移动的和所决定.2.平移的特征是:经过平移后的图形与原图形的对应线段,对应,图形的与都没有发生变化,即平移前后的两个图形;且对应点所连的线段.三、轴对称1.如果一个图形沿一条直线对折,对折后的两部分能,那么这个图形就是,这条直线就是它的.2.如果一个图形沿一条直线折叠,如果它能与另一个图形,那么这两个图形成,这条直线就是,折叠后重合的对应点就是.3.如果两个图形关于对称,那么对称轴是任何一对对应点所连线段的.定理1:关于某条直线对称的两个图形是全等形。定理2:如果两个图形关于某条直线对称,那么对称轴是对应点连线的垂直平分线。定理3:两个图形关于某条直线对称,如果它们的对应线段或延长相交。那么交点在对称轴上。逆定理:如果两个图形的对应点连线被一条直线垂直平分,那么这两个图形关于这条直线对称。四、旋转1.图形旋转的定义:把一个图形的图形变换,叫做旋转,叫做旋转中心,叫做旋转角.2.图形的旋转由、和所决定.其中①旋转点在旋转过程中保持不动.②旋转分为顺时针和逆时针.③旋转角一般小于360º.3.旋转的特征是:图形中每一点都绕着旋转了的角度,对应点到旋转中心的相等,对应相等,对应相等,图形的都没有发生变化.也就是旋转前后的两个图形.4.把一个图形绕着某一个点旋转°,如果旋转后的图形能够与原来的图形,那么这个图形叫做图形,这个点就是它的.5.把一个图形绕着某一个点旋转°,如果它能够与另一个图形,那么就说这两个图形关于这个点,这个点叫做.这两个图形中的对应点叫做关于中心的.6.关于中心对称的两个图形,对称点所连线段都经过,而且被对称中心所.关于中心对称的两个图形是图形.7.两个点关于原点对称时,它们的坐标符号,即点),(yxP关于原点的对称点1P为.【典型例题】1.如图所示的物体是一个几何体,其主视图是()12.在一个晴朗的上午,小丽拿着一块矩形木板在阳光下做投影实验,矩形木板在地面上形成的投影不可能是()3.如图是每个面上都有一个汉字的正方体的一种展开图,那么在正方体的表面,与“迎”相对的面上的汉字是()A.文B.明C.奥D.运4.右图是某一几何体的三视图,则这个几何体是()A.圆柱体B.圆锥体C.正方体D.球体5.如图,是一个由若干个相同的小正方体组成的几何体的三视图,则组成这个几何体的小正方体的个数是6.将图所示的RtABC△绕直角边AB旋转一周,所得几何体的主视图为()7.六个大小相同的正方体搭成的几何体如图所示,则关于它的视图说法正确的是()A.正视图的面积最大B.左视图的面积最大C.俯视图的面积最大D.三个视图的面积一样大8.下列几何图形中,一定是轴对称图形的有().A.2个B.3个C.4个D.5个9.下面四张扑克牌中,图案属于中心对称的是图中的()210.下列图形中,既是轴对称图形,又是中心对称图形的是()A.等腰梯形B.平行四边形C.正三角形D.矩形11.如图①~④是四种正多边形的瓷砖图案.其中,是轴对称图形但不是中心对称的图形为()A.①③B.①④C.②③D.②④12.如图,方格纸中有三个点ABC,,,要求作一个四边形使这三个点在这个四边形的边(包括顶点)上,且四边形的顶点在方格的顶点上.(1)在图甲中作出的四边形是中心对称图形但不是轴对称图形;(2)在图乙中作出的四边形是轴对称图形但不是中心对称图形;(3)在图丙中作出的四边形既是轴对称图形又是中心对称图形.13.如图,在直角坐标系xOy中,A(一l,5),B(一3,0),C(一4,3).(1)在右图中作出△ABC关于y轴的轴对称图形△A′B′C′;(2)如果ABC△中任意一点M的坐标为()xy,,那么它的对应点N的坐标是.14....