一三角函数的图像与性质VIP免费

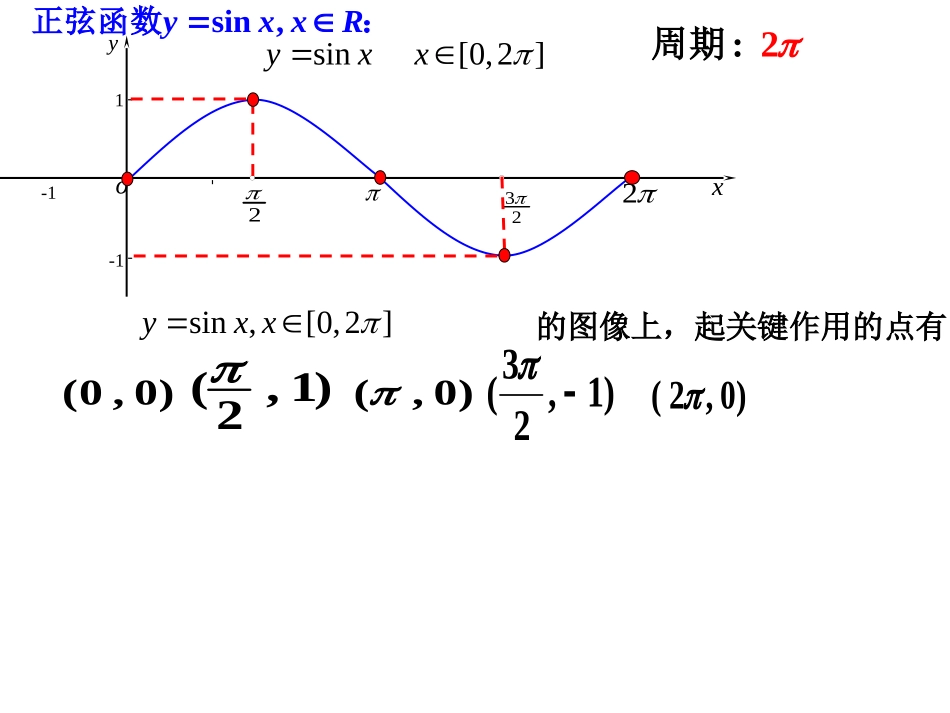
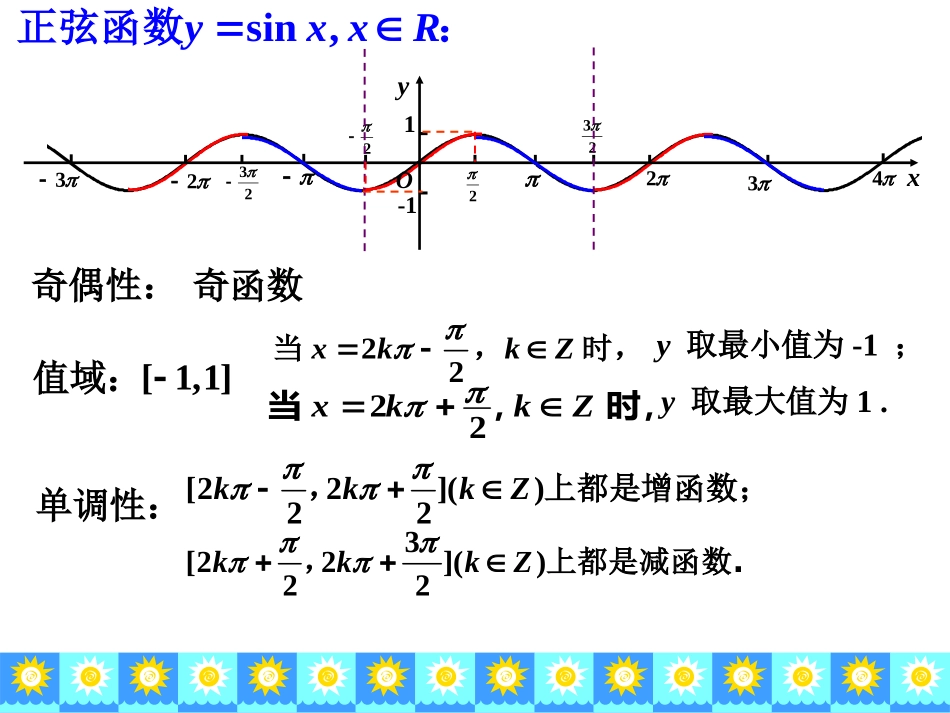
三角函数复习——正弦函数的性质与图像--1-oxy-1-12232sin[0,2]yxx在函数的图像上，起关键作用的点有：sin,[0,2]yxx3(,1)2)1,2(sin,yxxR正弦函数：2:周期(0,0)(,0)(2,0)Oyx22323422323-11sin,yxxR正弦函数：值域：[1,1]单调性：[22]()22kkkZ，上都是增函数；3[22]()22kkkZ，上都是减函数.y取最小值为-1；时，，当Zkkx2222xkkZ当，时，y取最大值为1.奇偶性：奇函数1()2sincos(),6fxxx例、已知函数求此函数的最值和单调区间.单名单角22()sin2+2cos+,(,),(1)fxxxaaRa例、已知函数是常数求此函数的周期；(2)[0,]2xa若时，此函数的最大值为1，求的值.(3)[0,]x求时，此函数的单调递增区间.sin,yxxR正弦函数：Oyx22323422323-11()2xkkZ对称轴：对称中心：(,0)()kkZsin1xsin0x2sin(2)13yx例3、求出函数的对称轴和对称中心；oxy判断其奇偶性.1()sin()3cos(),(0,0).2fxxxπ例4、已知函数为偶函数，且相邻两根对称轴的距离为，求此函数的解析式52|sin|sin1yxx例、已知函数（）求此函数的值域和单调区间；sin|cos|cos|sin|1[,]yxxxxx思考与练习：已知函数，（）作出此函数在内的大致图像；2.xR（）研究此函数在定义域上的最值和单调性2.（）此函数的函数图像是否具有对称轴，如果有，求出其对称轴方程cos,:yxxR余弦函数值域：:周期单调性：cos()(00)______yAxAA函数、、为常数，，的最小正周期是对称轴：对称中心：()3sin()cos(),(0,0).2fxxxπ2、已知函数为偶函数，且相邻两根对称轴的距离为，求此函数的解析式和对称中心及零点221()2sincos(1)2(2)();6333()44fxxxxx、已知函数求此函数的周期；若,，求此函数的值域（）若,的单调递减区间.3|cos|2cos.yxx、研究函数的性质补充练习：