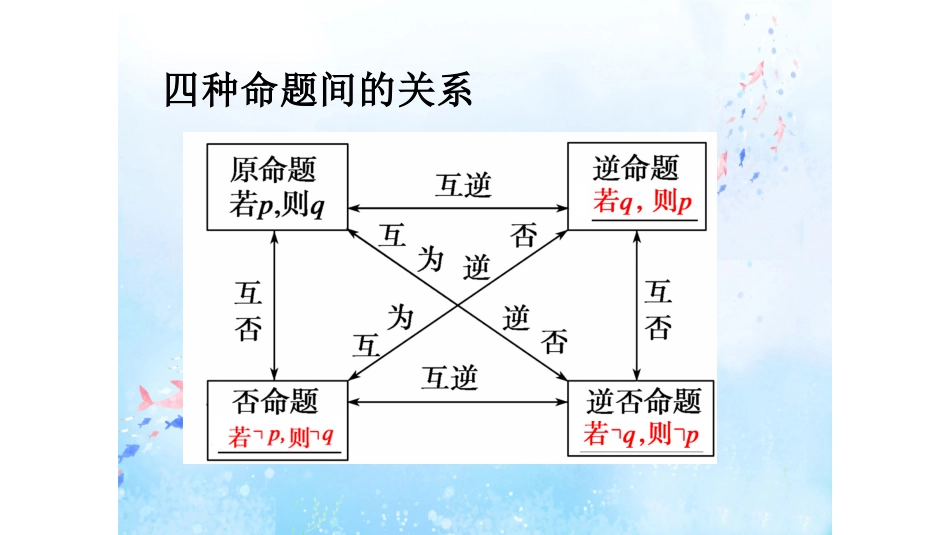
1.2.1充分条件与必要条件1.命题:一般地,我们把用表达的,可以的陈述句叫做命题.2.命题的真假:判断的语句叫真命题,判断的语句叫假命题.3.命题的形式:在数学中,“”是命题的常见形式,其中p叫做命题的,q叫做命题的.语言、符号或式子判断真假为真为假若p,则q条件结论复习回顾四种命题间的关系四种命题的真假性原命题逆命题否命题逆否命题真真真假假真假假真真真真假假假假四种命题真假性之间的关系(1)两个命题互为逆否命题,它们有的真假性;(2)两个命题为互逆命题或互否命题,它们的真假性.相同没有关系提问:鱼非常需要水,没了水,鱼就无法生存,但只有水,够吗?探究:p:“有水”;q:“鱼能生存”.判断“若p,则q”和“若q,则p”的真假.问题探究音乐欣赏:《我是一只鱼》(2)因为若ab=0则应该有a=0或b=0。所以并不能得到a一定为0。例:判断下列命题的真假。(1)若x>a2+b2,则x>2ab。(2)若ab=0,则a=0。真命题真命题假命题假命题解(1)因为若x>a2+b2,而a2+b22ab,所以可以得到x>2ab。定义新知命题真假“若p,则q”是真命题“若p,则q”是假命题推出关系PqPq条件关系p是q的条件q是p的条件p不是q的条件q不是p的条件充分充分必要必要充分条件与必要条件⇒例如:(1)因为若x>a2+b2,则x>2ab为真命题a=0不是ab=0的.所以:ab=0不是a=0的.所以:x>a2+b2是x>2ab的.(2)因为若ab=0,则a=0为假命题x>2ab是x>a2+b2的.即:x>a2+b2x>2ab即:ab=0a=0充分条件必要条件充分条件必要条件⇒⇒结合充分条件、必要条件的定义,说说你对充分条件与必要条件的理解.深化理解充分条件是使某一结论成立应该具备的条件,即要使此结论成立,只要具备此条件就足够了.必要条件可从命题等价性理解:pq⇒等价于﹁q⇒﹁p,意味着若q不成立,则p不成立,即q是p成立的必不可少的条件.有它,足以缺它,不可解:命题(1)(2)是真命题,命题(3)是假命题.所以,命题(1)(2)中的p是q的充分条件例1、下列“若p,则q”形式的命题中,哪些命题中的p是q的充分条件?(1)若x=1,则x2-4x+3=0;(2)若f(x)=x,则f(x)为增函数;(3)若x为无理数,则x2为无理数.巩固新知解:命题(1)(2)是真命题,命题(3)是假命题.所以,命题(1)(2)中的q是p的必要条件.例2、下列“若p,则q”形式的命题中,哪些命题中的q是p的必要条件?(1)若x=y,则x2=y2;(2)若x<3,则x<5;(3)若a>b,则ac>bc.(1)结合例1(1)例2(2),你能从集合的包含关系来判断充分条件与必要条件吗?(p对应的集合为P,q对应的集合为Q)提示:pq⇒,则PQ⊆,p是q的充分条件,q是p的必要条件。(2)若p是q的充分条件,p是唯一的吗?提示:不一定唯一,凡是能使q成立的条件都是它的充分条件,如x>3是x>0的充分条件,x>5,x>10等都是x>0的充分条件.(3)“若﹁p,则﹁q”为真命题,则p是q的什么条件?提示:“若﹁p,则﹁q”为真命题,则其逆否命题“若q,则p”也为真命题,即qp,⇒故p是q的必要条件.微思考类型一充分条件与必要条件的判断【典型习题】1.命题“已知n∈Z,若a=4n,则a是偶数”中,“a是偶数”是“a=4n”的条件,“a=4n”是“a是偶数”的条件(用充分、必要填空).小试牛刀【解析】1.命题“已知n∈Z,若a=4n,则a是偶数”是真命题,所以“a是偶数”是“a=4n”的必要条件,“a=4n”是“a是偶数”的充分条件.必要充分2.下列“若p,则q”形式的命题中:①若lgx=0,则2x=2;②若sinx=,则x=;③已知n∈N+,若an=2n,则{an}是等差数列.其中,p是q的充分条件的是,q是p的必要条件的是,p不是q的充分条件的是,q不是p的必要条件的是.(将符合题意的所有序号都填上)126真命题假命题真命题①③①③②②3.“x2=2x”是“x=0”的条件“x=0”是“x2=2x”的条件(用充分、必要填空).【解析】由于x=0x⇒2=2x,所以“x2=2x”是“x=0”的必要条件,“x=0”是“x2=2x”的充分条件.必要充分类型二充分条件与必要条件的应用【典型习题】1.若“x>1”是“x>a”的充分条件,则实数a的取值范围是()A.a>1B.a≥1C.a<1D.a≤1【解析】若“x>1”是“x>a”的充分条件,则x>1x>a,⇒于是{x|x>1}{x|x>a},⊆得a≤1.变式训练:若1中的“充分条件”改为“必要条件”,则实数a的取值范围________Da≥102.若“x=2”是“x2-2x+c=0”的充分条件,则c=....