二元一次不等式与平面区域(3)VIP免费

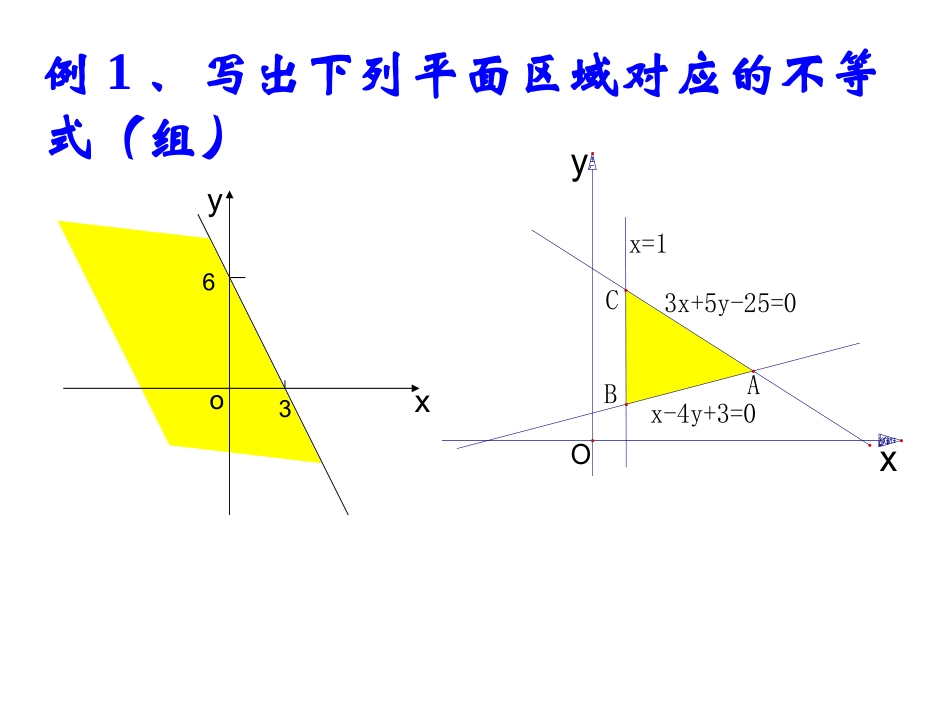
3.3.1二元一次不等式（组）与平面区域CBAx=1x-4y+3=03x+5y-25=0xOyxy36o例1、写出下列平面区域对应的不等式（组）例2、画出下列不等式表示的平面区域，并求其面积(1)4xy22(2)4xy(3)12xyx032:1yxl0632:2yxl01553:3yxlAll21Bll31Cll32)43,815(A)3,0(B)1912,1975(C解：设，，，，，，∴，，。于是看出区域内点的横坐标在内，取＝1，2，3，)1975,0(x当＝1时，代入原不等式组有⇒，1512y143125yyyx得＝－2，∴区域内有整点(1,-2)。同理可求得另外三个整点(2,0)，(2,-1)，(3,-1)。y例3、求不等式组的整数解015530632032yxyxyx小结：求不等式的整数解即求区域内的整点是教学中的难点，它为线性规划中求最优整数解作铺垫。常有两种处理方法，一种是通过打出网格求整点；另一种是先确定区域内点的横坐标x的范围，确定x的所有整数值，再代回原不等式组，得出y的一元一次不等式组，再确定y的所有整数值，即先固定x，再用x制约y。