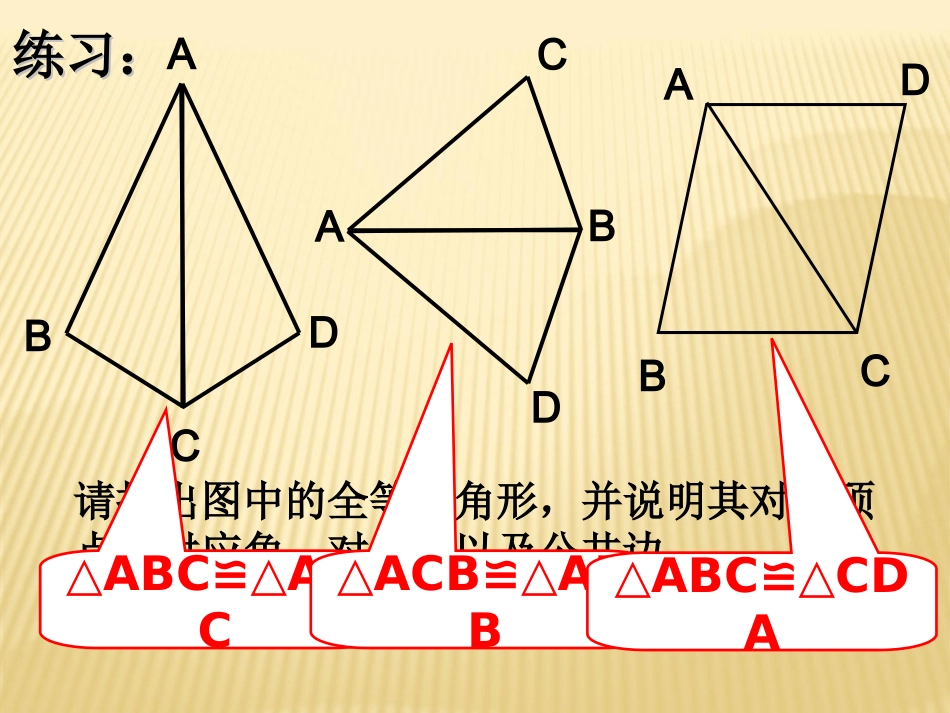
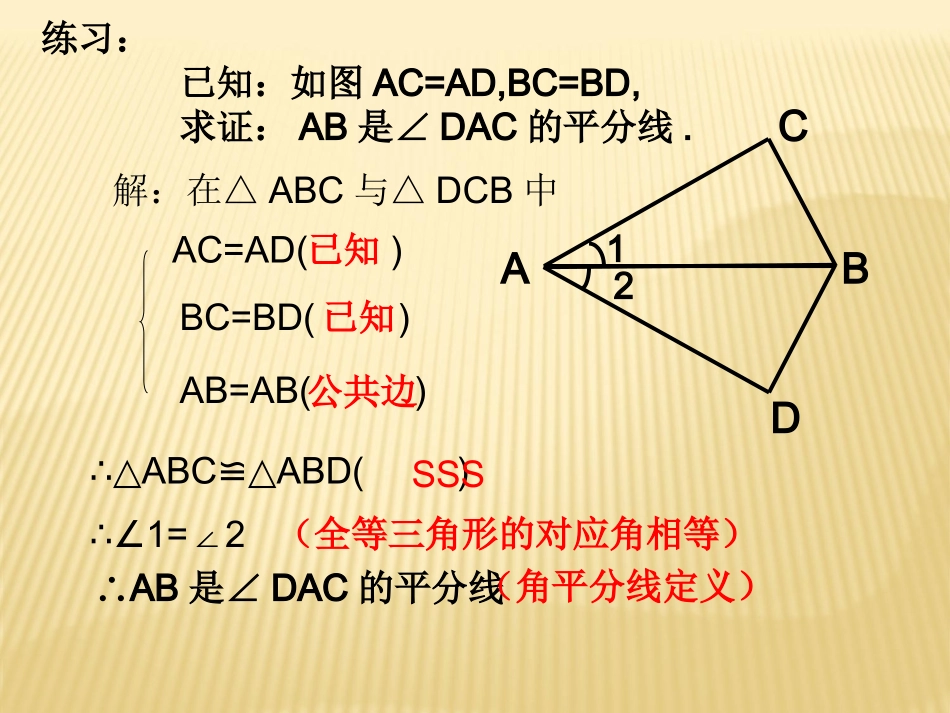
3.33.3探索三角形全等的条件探索三角形全等的条件(2)(2)ABCDABCD练习:练习:ADCB请找出图中的全等三角形,并说明其对应顶点,对应角、对应边以及公共边。△ABC≌△ADC△ACB≌△ADB△ABC≌△CDA练习:已知:如图AC=AD,BC=BD,求证:AB是∠DAC的平分线.AC=AD()BC=BD()AB=AB()∴△ABCABD()≌△∴∠1=2∠∴AB是∠DAC的平分线ABCD12(全等三角形的对应角相等)已知已知公共边SSS解:在△ABC与△DCB中(角平分线定义)如图如图,,小明不慎将一块三角形小明不慎将一块三角形模具打碎为两块模具打碎为两块,,他是否可以他是否可以只带其中的一块碎片到商店只带其中的一块碎片到商店去去,,就能配一块与原来一样的就能配一块与原来一样的三角形模具吗三角形模具吗??如果可以如果可以,,带带哪块去合适哪块去合适??你能说明其中理你能说明其中理由吗由吗??全等三角形判定条件2几何语言:在△ABC与△DEF中∠B=∠E(已知)BC=EF(已知)∠C=∠F(已知)∴ΔABC≌DEF(ASASAA)AABBCCDDEEFF探究探究&&新新知知☞☞两角和它们的夹边对应相等的两个三角形全等。简写成“角边角”或“ASA”。如图如图,,小明不慎将一块三角形模具打碎为两块小明不慎将一块三角形模具打碎为两块,,他是否可以只带其中的一块碎片到商店去他是否可以只带其中的一块碎片到商店去,,就能就能配一块与原来一样的三角形模具吗配一块与原来一样的三角形模具吗??如果可以如果可以,,带哪块去合适带哪块去合适??你能说明其中理由吗你能说明其中理由吗??ⅠⅡ三角形全等判定条件3几何语言:在△ABC与△DEF中∠B=∠E(已知)∠C=∠F(已知)AC=DF(已知)∴ΔABC≌DEF(AASAAS)探究探究&&新新知知☞☞AABBCCDDEEFF两角和其中一角的对边对应相等的两个三角形全等。简写成“角角边”或“AAS”。1、如图,已知AB=DE,∠A=D∠,,B=E∠∠,则△ABCDEF△的理由是:2、如图,已知AB=DE,A=D∠∠,,C=F∠∠,则△ABCDEF△的理由是:ABCDEF角边角(ASA)角角边(AAS)应用新知,体验成功3、如图,AB=AC,∠B=∠C求证:△ABE≌△ACD证明:在△ABE与△ACD中∠B=∠C(已知)AB=AC(已知)∠A=∠A(公共角)∴△ABE≌△ACD(ASA)AEDCBBE=CD4.4.如图如图,O,O是是ABAB的中点,的中点,=.=.证明:与全等证明:与全等ABAOCBODOABCDBABOAOBODAOCBODAOC)(ASABODAOC和((已知已知))((已证已证))((对顶角相等对顶角相等))在和中在和中()()证明:∴AO=BO(AO=BO(中点定义中点定义))∵∵OO是是ABAB的中点(已知)的中点(已知)AC=BD