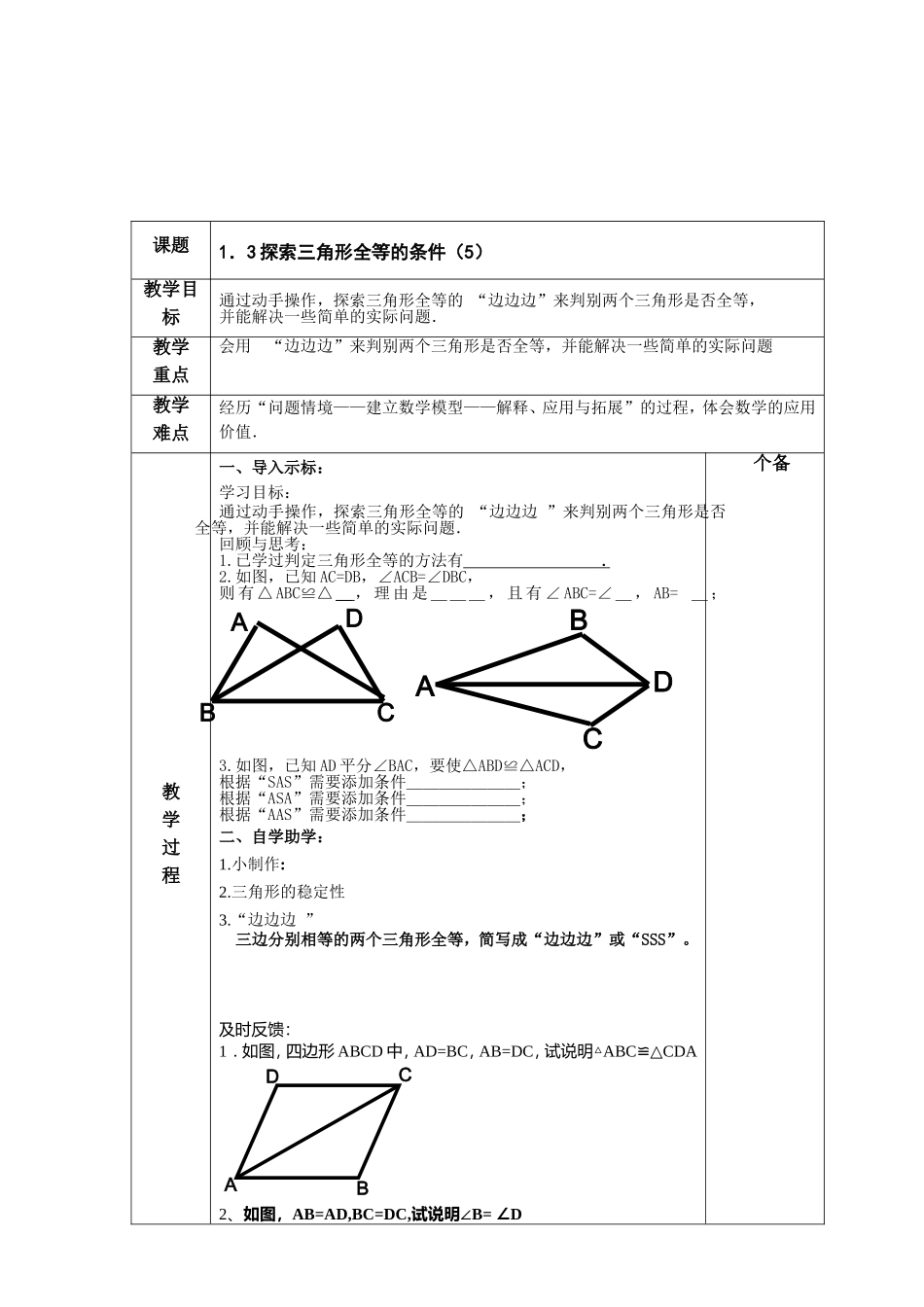
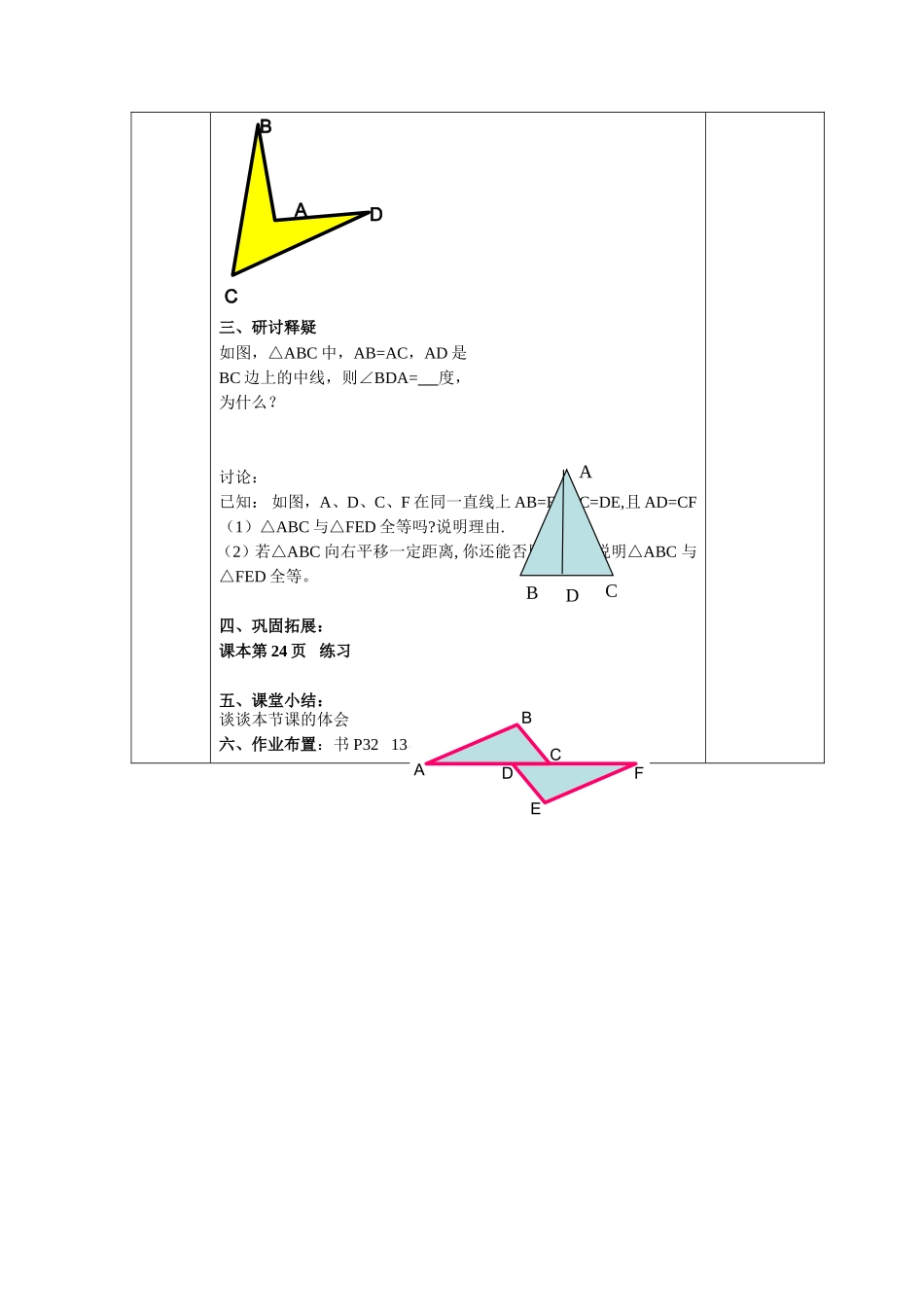
江南学校“导学研练”高效课堂教学案八年级数学学科(第二稿)主备:凌锁川图8课题1.3探索三角形全等的条件(5)教学目标通过动手操作,探索三角形全等的“边边边”来判别两个三角形是否全等,并能解决一些简单的实际问题.教学重点会用“边边边”来判别两个三角形是否全等,并能解决一些简单的实际问题教学难点经历“问题情境——建立数学模型——解释、应用与拓展”的过程,体会数学的应用价值.教学过程一、导入示标:学习目标:通过动手操作,探索三角形全等的“边边边”来判别两个三角形是否全等,并能解决一些简单的实际问题.回顾与思考:1.已学过判定三角形全等的方法有.2.如图,已知AC=DB,∠ACB=∠DBC,则有△ABC≌△_,理由是___,且有∠ABC=∠_,AB=_;3.如图,已知AD平分∠BAC,要使△ABD≌△ACD,根据“SAS”需要添加条件_______;根据“ASA”需要添加条件_______;根据“AAS”需要添加条件_______;二、自学助学:1.小制作:2.三角形的稳定性3.“边边边”三边分别相等的两个三角形全等,简写成“边边边”或“SSS”。及时反馈:1.如图,四边形ABCD中,AD=BC,AB=DC,试说明△ABC≌△CDA2、如图,AB=AD,BC=DC,试说明∠B=∠D个备ABCDABCDABCD三、研讨释疑如图,△ABC中,AB=AC,AD是BC边上的中线,则∠BDA=度,为什么?讨论:已知:如图,A、D、C、F在同一直线上AB=EF,BC=DE,且AD=CF(1)△ABC与△FED全等吗?说明理由.(2)若△ABC向右平移一定距离,你还能否用“SSS”说明△ABC与△FED全等。四、巩固拓展:课本第24页练习五、课堂小结:谈谈本节课的体会六、作业布置:书P3213、14、P324ABCDADCBEFDABC