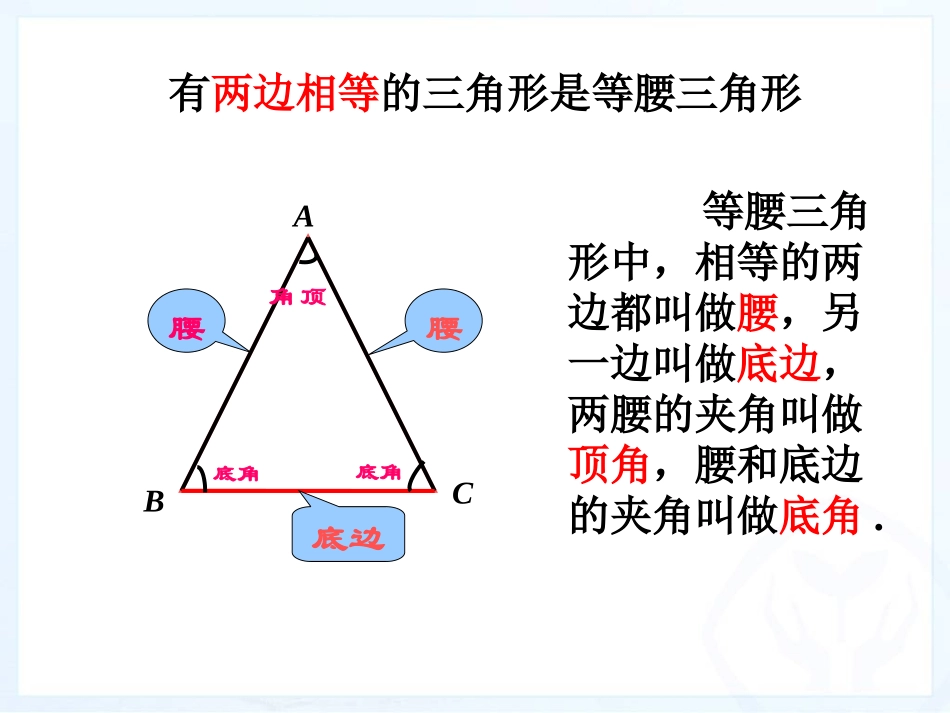
八年级上册13.3.1等腰三角形(第1课时)等腰三角形中,相等的两边都叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.ACB腰腰底边顶角底角底角有两边相等的三角形是等腰三角形如图所示,把一张长方形的纸按图中虚线对折,并剪去阴影部分,再把它展开,得到的△ABC有什么特点?探索等腰三角形的性质ABCD把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角。由这些重合的线段和角,你能发现等腰三角形的性质吗?说说你的猜想。探索等腰三角形的性质ABCDABCD等腰三角形的特征:(1)等腰三角形的两个底角相等;(2)等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.探索等腰三角形的性质在练习本上任意画一个等腰三角形,把它剪下来,折一折,上面得出的结论仍然成立吗?由此你能概括出等腰三角形的性质吗?探索等腰三角形的性质同学们剪下的等腰三角形纸片大小不同,形状各异,是否都具有上述所概括的特征?探索等腰三角形的性质等腰三角形的性质:(1)等腰三角形的两个底角相等;(等边对等角)(2)等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.利用实验操作的方法,我们发现并概括出等腰三角形的性质1和性质2.对于性质1,你能通过严格的逻辑推理证明这个结论吗?(1)你能根据结论画出图形,写出已知、求证吗?(2)结合所画的图形,你认为证明两个底角相等的思路是什么?(3)如何在一个等腰三角形中构造出两个全等三角形呢?从剪图、折纸的过程中你能获得什么启发?探索并证明等腰三角形的性质已知:如图,△ABC中,AB=AC.求证:∠B=∠C.探索并证明等腰三角形的性质ABCD证明:作底边的中线AD.∵AD是底边BC的中线,∴BD=CD.∵AB=AC,BD=CD,AD=AD,∴△ABD≌△ACD(SSS).∴∠B=∠C.你还有其他方法证明性质1吗?探索并证明等腰三角形的性质可以作底边的高线或顶角的角平分线.ABCD性质2可以分解为三个命题,本节课证明“等腰三角形的底边上的中线也是底边上的高和顶角平分线”.探索并证明等腰三角形的性质性质2.等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.ABCD已知:如图,△ABC中,AB=AC,AD是底边BC的中线.求证:∠BAD=∠CAD,AD⊥BC.探索并证明等腰三角形的性质ABCD证明:∵AD是底边BC的中线,∴BD=CD.∵AB=AC,BD=CD,AD=AD,∴△ABD≌△ACD(SSS).∴∠BAD=∠CAD∠ADB=∠ADC.∵∠ADB+∠ADC=180°,∴∠ADB=90°.∴AD⊥BC.探索并证明等腰三角形的性质在等腰三角形性质的探索过程和证明过程中,“折痕”“辅助线”发挥了非常重要的作用,由此,你能发现等腰三角形具有什么特征?等腰三角形是轴对称图形,底边上的中线(顶角平分线、底边上的高)所在直线就是它的对称轴.课堂练习练习1填空:(1)如图,△ABC中,AB=AC,∠A=36°,则∠B=°;ABC课堂练习练习1填空:(2)如图,△ABC中,AB=AC,∠B=36°,则∠A=°;ABC课堂练习练习1填空:(3)已知等腰三角形的一个内角为70°,则它的另外两个内角的度数分别是.精讲点拨例如图,△ABC中,AB=AC,点D在AC上,且BD=BC=AD.求△ABC各角的度数.ABCD解:∵AB=AC,BD=BC=AD,∴∠ABC=∠C=∠BDC,∠A=∠ABD(等边对等角)设∠A=x,则∠BDC=∠A+∠ABD=2x,从而∠ABC=∠C=∠BDC=2x,于是在△ABC中,有∠A+∠ABC+∠C=x+2x+2x=180°.解得x=36°,在△ABC中,∠A=36°,∠ABC=∠C=72°.(1)本节课学习了哪些主要内容?(2)我们是怎么探究等腰三角形的性质的?(3)本节课你学到了哪些证明线段相等或角相等的方法?课堂小结教科书习题13.3第1、2、4、6题.布置作业