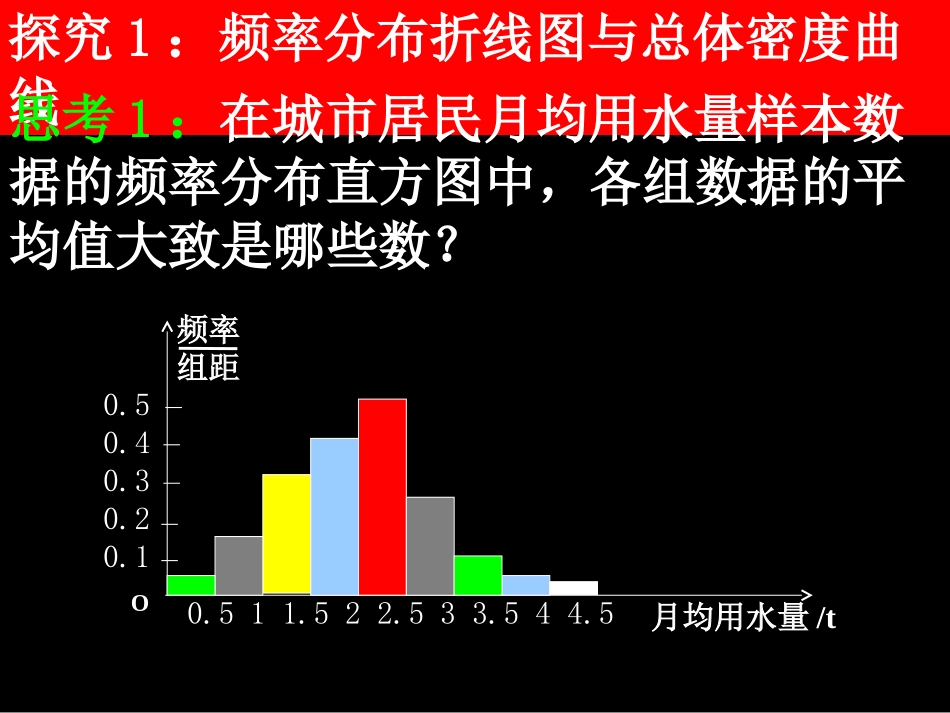
探究1:频率分布折线图与总体密度曲线思考1:在城市居民月均用水量样本数据的频率分布直方图中,各组数据的平均值大致是哪些数?月均用水量/t频率组距0.50.40.30.20.10.511.522.533.544.5O思考2:在频率分布直方图中,依次连接各小长方形上端的中点,就得到一条折线,这条折线称为频率分布折线图.你认为频率分布折线图能大致反映样本数据的频率分布吗?月均用水量/t频率组距0.50.40.30.20.10.511.522.533.544.5O思考3:当总体中的个体数很多时(如抽样调查全国城市居民月均用水量),随着样本容量的增加,作图时所分的组数增多,组距减少,你能想象出相应的频率分布折线图会发生什么变化吗?月均用水量/t频率组距0.50.40.30.20.10.511.522.533.544.5O月均用水量/t频率组距abO总体密度曲线思考4:在上述背景下,相应的频率分布折线图越来越接近于一条光滑曲线,统计中称这条光滑曲线为总体密度曲线.那么图中阴影部分的面积有何实际意义?总体在区间(a,b)内取值的百分比.思考5:当总体中的个体数比较少或样本数据不密集时,是否存在总体密度曲线?为什么?不存在,因为组距不能任意缩小.思考6:对于一个总体,如果存在总体密度曲线,这条曲线是否惟一?能否通过样本数据准确地画出总体密度曲线?探究(二):茎叶图频率分布表、频率分布直方图和折线图的主要作用是表示样本数据的分布情况,此外,我们还可以用茎叶图来表示样本数据的分布情况.【问题】某赛季甲、乙两名篮球运动员每场比赛的得分情况如下:甲运动员得分:13,51,23,8,26,38,16,33,14,28,39;乙运动员得分:49,24,12,31,50,31,44,36,15,37,25,36,39.助教在比赛中将这些数据记录为如下形式:甲乙846336838910123452554661679490甲乙846336838910123452554661679490思考1:你能理解这个图是如何记录这些数据的吗?你能通过该图说明哪个运动员的发挥更稳定吗?甲运动员得分:13,51,23,8,26,38,16,33,14,28,39;乙运动员得分:49,24,12,31,50,31,44,36,15,37,25,36,39.思考2:在统计中,上图叫做茎叶图,它也是表示样本数据分布情况的一种方法,其中“茎”指的是哪些数,“叶”指的是哪些数?甲乙846336838910123452554661679490思考3:对于样本数据:3.1,2.5,2.0,0.8,1.5,1.0,4.3,2.7,3.1,3.5,用茎叶图如何表示?012348050571153茎叶思考4:一般地,画出一组样本数据的茎叶图的步骤如何?第一步,将每个数据分为“茎”(高位)和“叶”(低位)两部分;第二步,将最小的茎和最大的茎之间的数按大小次序排成一列,写在左(右)侧;第三步,将各个数据的叶按大小次序写在茎右(左)侧.思考5:用茎叶图表示数据的分布情况是一种好方法,你认为茎叶图有哪些优点?(1)保留了原始数据,没有损失样本信息;(2)数据可以随时记录、添加或修改.思考6:比较茎叶图和频率分布表,茎叶图中“茎”和“叶”的数目分别与频率分布表中哪些数目相当?思考7:对任意一组样本数据,是否都适合用茎叶图表示?为什么?不适合样本容量很大或茎、叶不分明的样本数据.知识迁移例1在某小学500名学生中随机抽样得到100人的身高如下表(单位cm):461015人数[154,158)[150,154)[146,150)[142,146)身高区间2818982人数[138,142)[134,138)[130,134)[126,130)[122,126)身高区间(1)列出样本频率分布表;(2)画出频率分布直方图;(3)估计该校学生身高小于134cm的人数约为多少?(1)频率分布表:分组频数频率[122,126)2[126,130)8[130,134)9[134,138)18[138,142)28[142,146)15[146,150)10[150,154)6[154,158)4合计1001.000.020.080.090.180.280.150.100.060.04(2)频率分布直方图:身高/cm0.080.070.060.050.040.030.020.01122126130134138142146150154158频率组距O(3)(0.02+0.08+0.09)×500=95(人)例2为了了解高一学生的体能情况,某校随机抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出了频率分布直方图.图中从左到右各小长方形的面积之比为2:4:17:15:9:3,第二小组的频数为12.(1)第二小组的频率是多少?(2)样本容量是多少?...