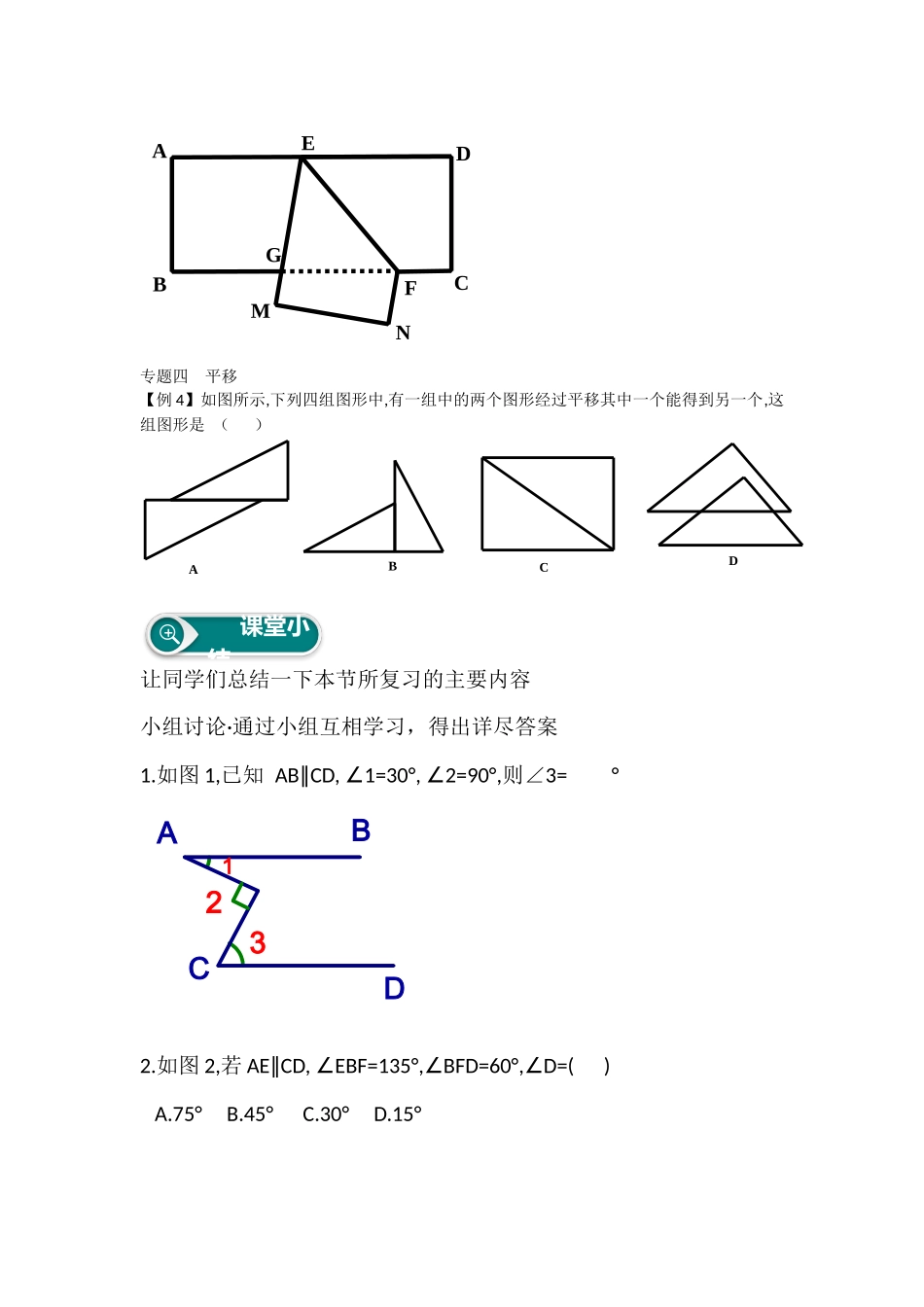
教学过程设计【教学过程】一、抽同学回忆平行线的性质和判定,给学生意知识的完整性学生归纳。为后面的练习准备.二、1、2题是平行线的性质和判定的简单应用。给学生以回忆的时间。活动1问题讨论:-我们知道两条平行线被第三条直线所截,不但形成有同位角,还有内错角、同旁内角.我们已经知道“两条平行线被第三条直线所截,同位角相等”.那么请同学们想一想:两条平行线被第三条直线所截,内错角、同旁内角有什么关系?(分组讨论,每一小组推荐一位同学回答).教师活动设计:引导学生讨论并回答.学生口答,教师板书,并要求学生学习推理的书写格式.活动2总结平行线的性质.性质2:两条平行线被第三条直线所截,内错角相等.简单说成:两直线平行,内错角相等.性质3:两条平行直线被第三条直线所截,同旁内角互补.简单说成:两直线平行,同旁内角互补.(老师强调书写)专题三平行线的性质和判定的应用:【例3】(1)如图所示,1=72°,2=72°,3=60°,∠∠∠求∠4的度数.三、拓展创新、应用提高,引导学生运用知识解决问题,培养学生思维的灵活性和深刻性【归纳拓展】平行线的性质和判定经常结合使用,由角之间的关系得出直线平行,进而再得出其他角之间的关系,或是由直线平行得到角之间的关系,进而再由角的关系得出其他直线平行.【迁移应用3】如图所示,把一张张方形纸片ABCD沿EF折叠,若∠EFG=50°,求∠DEG的度数.4321baNMFGEDCBA专题四平移【例4】如图所示,下列四组图形中,有一组中的两个图形经过平移其中一个能得到另一个,这组图形是()DCBA让同学们总结一下本节所复习的主要内容小组讨论·通过小组互相学习,得出详尽答案1.如图1,已知ABCD,1=30°,2=90°,∥∠∠则∠3=°321DCBA2.如图2,若AECD,EBF=135°,BFD=60°,D=()∥∠∠∠A.75°B.45°C.30°D.15°课堂小结FDCEBA3、已知:如图ABCD,∥试探究∠BED与∠B,D∠的关系?ABEDC教师活动设计:这个问题是平行线的特征与直线平行的条件的综合应用.由两直线平行,得到角的关系用到的是平行线的特征;反过来,由角的关系得到两直线平行,用到的是直线平行的条件.同学们要弄清这两者的区别.(利用小组讨论的方法,多给学生时间将学生的书写用照片的形式展示,学生进行相互评价。)〔解答〕略.问题4:如图,若AB//CD,你能确定∠B、∠D与∠BED的大小关系吗?说说你的看法.FBDCEA学生活动设计:由于有平行线,所以要用平行的知识,而∠B、∠D与∠DEB这三个角不是三类角中的任何一类,因此要考虑构造图形,若过点E作EF//AB,则由AB//CD得到EF//CD,于是图中出现三条平行线,同时出现了三类角,根据平行线的性质可以得到:∠B=∠BEF、∠D=∠DEF,因此∠B+∠D=∠BEF+∠DEF=∠DEB.教师活动设计:在学生探索的过程中,特别是构造图形这个环节,适当引导,让学生养成“缺什么补什么”的意识,培养学生的逻辑推理能力.〔解答〕过点E作EF//AB.ABEDC所以∠B=∠BEF.因为AB//CD.所以EF//CD.所以∠D=∠DEF.所以∠B+∠D=∠BEF+∠DEF=∠DEB.即∠B+∠D=∠DEB.变式思考:如图,AB//CD,探索∠B、∠D与∠BED的大小关系(∠B+∠D+∠DEB=360°).EDCBA四、小结与作业.小结:1.平行线的三个性质:两直线平行,同位角相等.两直线平行,内错角相等.两直线平行,同旁内角互补.2.平行线的性质与平行线的判定有什么区别?判定:已知角的关系得平行的关系.证平行,用判定.性质:已知平行的关系得角的关系.知平行,用性质.作业:习题5.3.