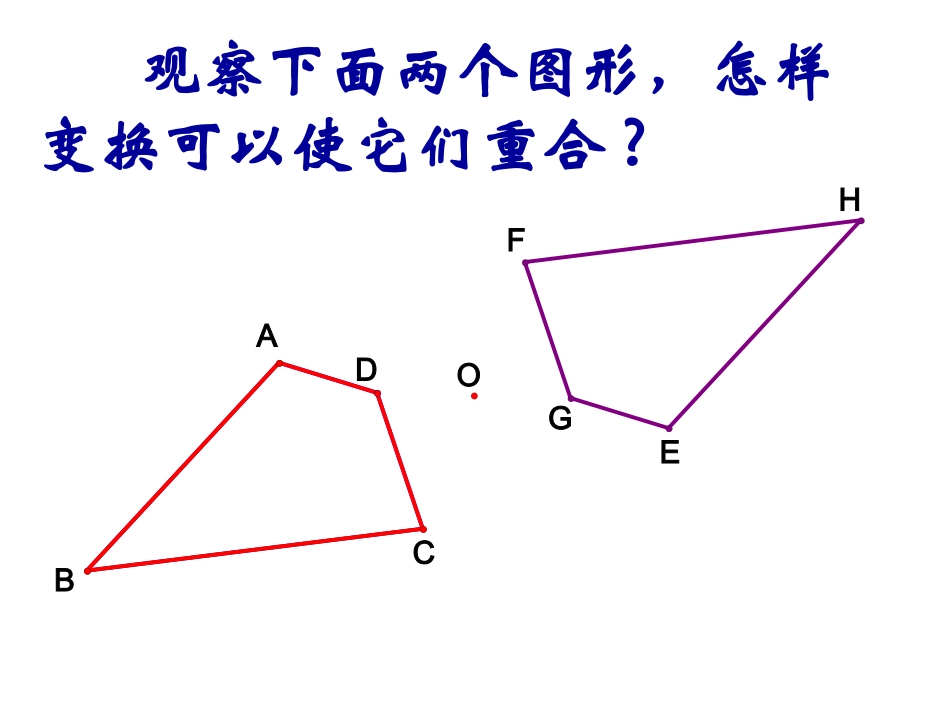
八年级数学(下)§9.2中心对称与中心对称图形(1)第9章中心对称图形——平行四边形观察下列各组图形,你能发现什么?观察下面两个图形,怎样变换可以使它们重合?GFEHABCOD把一个图形绕某一点旋转1800,如果它能够与另一个图形重合,那么称这两个图形关于这点对称,也称这两个图形成中心对称,这个点叫做对称中心,两个图形中的对应点叫做对称点.中心对称一个图形绕某一点旋转1800是一种特殊的旋转,因此成中心对称的两个图形具有图形旋转的一切性质.中心对称中心对称还有哪些性质呢?成中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分.中心对称的性质成中心对称的两个图形,对应角相等,对应线段相等且平行(或在同一条直线上).(这与平移一样)想一想中心对称与轴对称有什么区别?又有什么联系?轴对称中心对称有一条对称轴---直线有一个对称中心---点图形沿对称轴对折(翻折1800)后重合图形绕对称中心旋转1800后重合对称点的连线被对称轴垂直平分对称点连线经过对称中心,且被对称中心平分如图,2块同样的三角尺,它们是否关于某点成中心对称?若是,请确定它的对称中心.例1想一想如果两图形的对应点连线都经过某一点,并且都被这一点平分,那么它们关于这一点对称.如何判断两个图形是否关于某点对称呢?想一想1.如何作点A关于点O的对称点?2.如何作线段AB关于点O的对称线段?如图,已知△ABC和点O,画出△DEF,使它与△ABC关于点O成中心对称.例2CABFEGO如图,D是△ABC的边AC上一点,画出△EFG,使它与ABC点D成中心对称.练习BCAD如图,是一个6×6的棋盘,两人各持若干张1×2的卡片轮流在棋盘上盖卡片,每人每次用一张卡片盖住相邻的两个空格,谁找不出相邻的两个空格放卡片就算谁输,你用什么办法战胜对手呢?思维拓展