1.4.2正弦函数、余弦函数的性质(第1课时)VIP免费

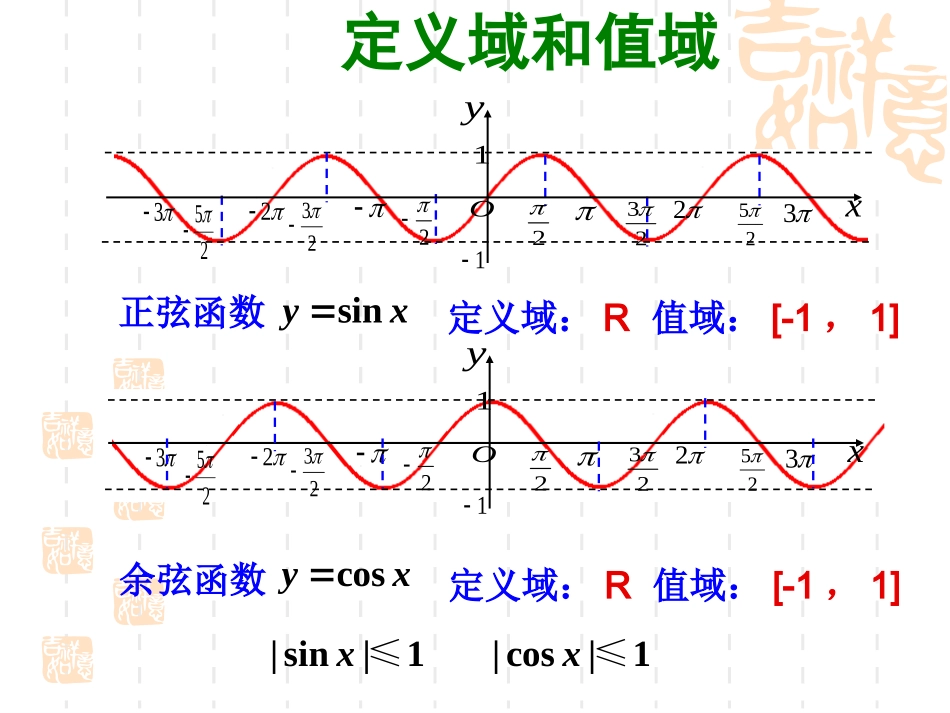
三角函数1.4.2正弦函数余弦函数的性质（一）定义域和值域x22322523yO23225311x22322523yO23225311正弦函数sinyx定义域：R值域：[-1，1]余弦函数cosyx定义域：R值域：[-1，1]|sin|1|cos|1≤≤xx练习P46练习2(1)2cos3x2(2)sin0.5x3cos2x1×sin0.5x[1,1]√1.周期性（复习）(1)sinyx2Tsin()yAx2||T(2)cosyx2Tcos()yAx2||T练习已知函数的周期是3，且当时，，求()yfx[0,3]x2()1fxx(1),(5),(16).fff思考：吗？2(5)5126f2.奇偶性(1)()sin,fxxxRxR任意()sin()fxxsinx()fx()sin,fxxxR为奇函数(2)()cos,fxxxRxR任意()cos()fxxcosx()fx()cos,fxxxR为偶函数正弦函数的图象探究余弦函数的图象问题：它们的图象有何对称性？x22322523yO23225311x22322523yO232253112.奇偶性中心对称：将图象绕对称中心旋转180度后所得的曲线能够和原来的曲线重合。轴对称：将图象绕对称轴折叠180度后所得的曲线能够和原来的曲线重合。x22322523yO23225311P'P正弦函数的图象53113,,,,22222x对称轴：,2xkkZ(,0),(0,0),(,0),(2,0)对称中心：(,0)kkZ余弦函数的图象,0,,2x对称轴：,xkkZ35(,0),(,0),(,0),(,0)2222对称中心：(,0)2kkZ'PPx22322523yO23225311练习为函数的一条对称轴的是（）sin(2)3yxx22322523yO232253114.3Ax12x.2Bx.0Dx解：经验证，当.12Cx时232x12x为对称轴例题求函数的对称轴和对称中心sin(2)3yx23zx解（1）令则sin(2)sin3yxzsinyz的对称轴为,2zkkZ232xk解得：对称轴为,122xkkZ(2)sinyz的对称中心为(,0),kkZ23xk对称中心为62xkzk(,0),Z62kk练习求函数的对称轴和对称中心1cos()24yxx22322523yO23225311P'P正弦函数的图象53113,,,,22222x对称轴：,2xkkZ(,0),(0,0),(,0),(2,0)对称中心：(,0)kkZ小结余弦函数的图象,0,,2x对称轴：,xkkZ35(,0),(,0),(,0),(,0)2222对称中心：(,0)2kkZ'PPx22322523yO23225311作业求函数的对称轴和对称中心P53A10cos(2)3yx