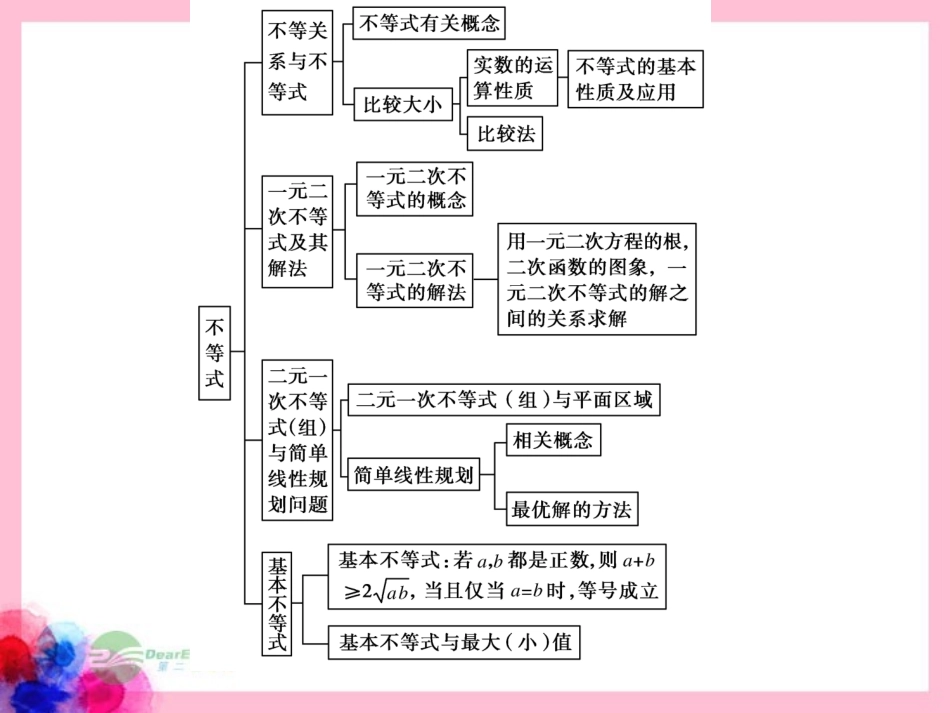
1.了解现实世界和日常生活中存在着大量的不等关系,了解不等式(组)的实际背景.2.会从实际情境中抽象出一元二次不等式模型.3.通过函数图象了解一元二次不等式与相应的二次函数、一元二次方程的联系.4.会解一元二次不等式,对给定的一元二次不等式,会设计求解的程序框图.5.会从实际情境中抽象出二元一次不等式组.6.了解二元一次不等式的几何意义,能用平面区域表示二元一次不等式组.7.会从实际情境中抽象出一些简单的二元线性规划问题,并能加以解决.8.了解基本不等式的证明过程.9.会用基本不等式解决简单的最大(小)值问题.1.不等式的性质是证明不等式、解不等式、求函数定义域等问题必须遵循的依据,必须牢固掌握并会进行推导.2.不等式的解法是高考必考内容,要熟练掌握简单不等式的解法,特别是一元二次不等式的解法,同时兼顾二次方程的判别式、根的存在性等知识.3.线性规划问题是高考的热点问题.主要考查平面区域的表示,用图解法解决线性规划问题,应以课本为主,要善于把二元一次不等式组用平面区域表示出来;还要善于把其他的不等式组转化为二元不等式组,然后利用“直线定界、原点定域”,作出线性区域.掌握从实际问题中抽象出线性规划模型的方法和技巧.4.基本不等式是每年高考的热点,但严格限制在两个以下.应用基本不等式求最值或证明不等式时应注意“一正、二定、三相等”的条件.1.利用不等式的性质、不等式的证明方法、解不等式等知识可以解决函数中的有关问题,主要体现在:利用不等式求函数的定义域、值域、最值、证明单调性等.2.利用函数、方程、不等式之间的关系,可解决一元二次方程根的分布及相关的不等式问题.已知函数f(x)=log3mx2+8x+nx2+1的定义域为R,值域为[0,2],求m,n的值.解析:令y=mx2+8x+nx2+1, 函数f(x)的定义域为R,∴对任意实数x∈R,y>0恒成立,即mx2+8x+n>0恒成立.当m=0时,不等式化为8x>-n,不可能恒成立;当m≠0时,必须有m>0,Δ=64-4mn<0,即m>0,mn>16.由y=mx2+8x+nx2+1得(m-y)x2+8x+(n-y)=0. x∈R,∴Δ=82-4(m-y)(n-y)≥0,即y2-(m+n)y+mn-16≤0①∴m+n=10mn-16=9,∴m=5n=5.此时满足m>0mn>16.故所求m=5,n=5.由题意知f(x)∈[0,2],则y∈[1,9].即关于y的不等式①的解集为[1,9].不等式恒成立,求参数的取值范围,一般有三种常用方法:(1)直接将参数从不等式中分离出来变成k≥f(x)(或k≤f(x)),从而转化成f(x)求最值.(2)如果参数不能分离,而x可以分离,如g(x)≥f(k)(或g(x)≤f(k)),则f(k)恒大于g(x)的最大值或恒小于g(x)的最小值,然后解关于参数k的不等式.(3)若不等式对于x,参数都是二次的,则借助二次函数在某区间上恒大于0或恒小于0,求解.已知f(x)=x2-2ax+2(a∈R),当x∈[-1,+∞)时,f(x)≥a恒成立,求a的取值范围.解析:方法一:f(x)=(x-a)2+2-a2,此二次函数图象的对称轴为x=a.①当a∈(-∞,-1)时,f(x)在[-1,+∞)上单调递增,f(x)min=f(-1)=2a+3.要使f(x)≥a恒成立,只需f(x)min≥a,即2a+3≥a,解得-3≤a<-1;②当a∈[-1,+∞)时,f(x)min=f(a)=2-a2,由2-a2≥a,解得-1≤a≤1.综上所述,所求a的取值范围为-3≤a≤1.方法二:令g(x)=x2-2ax+2-a,由已知,得x2-2ax+2-a≥0在[-1,+∞)上恒成立,设f(x)=mx2-mx-6+m.(1)若对于m∈[-2,2],f(x)<0恒成立,求实数x的取值范围;(2)若对于x∈[1,3],f(x)<0恒成立,求实数m的取值范围.解析:(1)依题意,设g(m)=(x2-x+1)m-6,则g(m)是关于m的一次函数,且一次项系数x2-x+1=x-122+34>0,∴g(m)在[-2,2]上递增.∴欲使f(x)<0恒成立,需g(m)max=g(2)=2(x2-x+1)-6<0,解得x的取值范围为-1<x<2.方法二:要使f(x)=m(x2-x+1)-6<0在x∈[1,3]上恒成立,则有m<6x2-x+1在x∈[1,3]上恒成立.而当x∈[1,3]时,6x2-x+1=6x-122+34≥67.∴m<6x2-x+1min=67,∴m<67.求目标函数在约束条件下的最优解,一般步骤...