高三数学：《一次函数》综合练习课件VIP免费

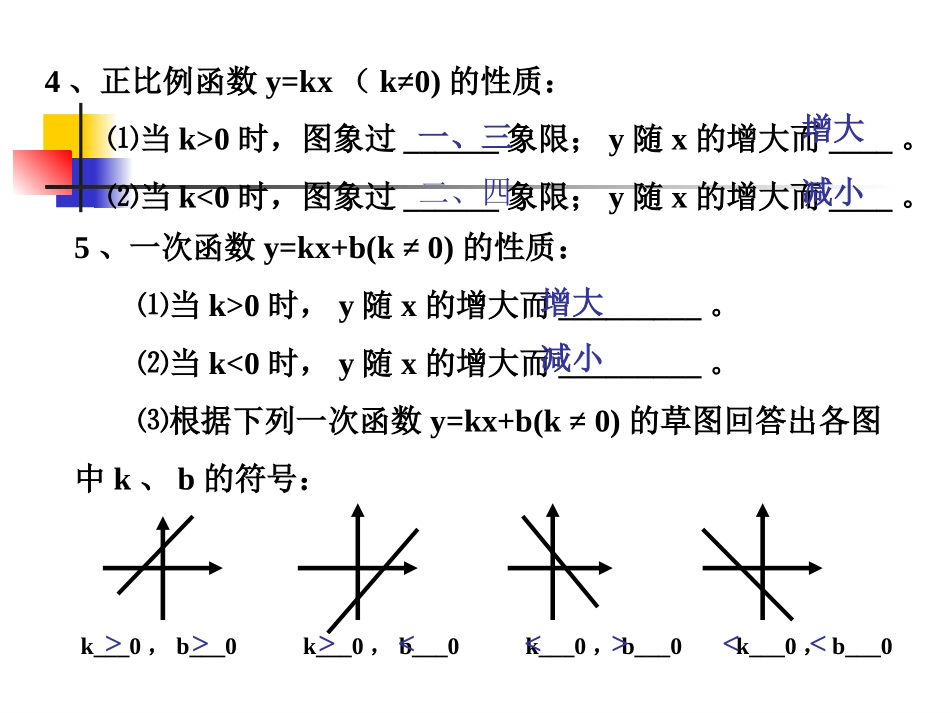
一、知识要点：1、一次函数的概念：函数y=_______(k、b为常数，k______)叫做一次函数。当b_____时，函数y=____(k____)叫做正比例函数。kx＋b≠０=０≠０kx★理解一次函数概念应注意下面两点：⑴、解析式中自变量x的次数是___次，⑵、比例系数_____。1K≠02、正比例函数y=kx(k≠0)的图象是过点（_____），(______)的_________。3、一次函数y=kx+b(k≠0)的图象是过点（0，___),（____，0)的__________。0，01，k一条直线b一条直线kb4、正比例函数y=kx（k≠0)的性质：⑴当k>0时，图象过______象限；y随x的增大而____。⑵当k<0时，图象过______象限；y随x的增大而____。一、三增大二、四减小5、一次函数y=kx+b(k≠0)的性质：⑴当k>0时，y随x的增大而_________。⑵当k<0时，y随x的增大而_________。⑶根据下列一次函数y=kx+b(k≠0)的草图回答出各图中k、b的符号：增大减小k___0，b___0k___0，b___0k___0，b___0k___0，b___0<<><<>>>二、范例。例１填空题：(1)有下列函数：①,②,③,④。其中过原点的直线是_____；函数y随x的增大而增大的是___________；函数y随x的增大而减小的是______；图象在第一、二、三象限的是_____。56xy4xy34xy②①、②、③④③(2)、如果一次函数y=kx-3k+6的图象经过原点，那么k的值为________。（3）如果一次函数y=kx-3k+6的图象平行与直线Y=3x-4则K的值为。(4)、已知y-1与x成正比例，且x=－2时，y=4，那么y与x之间的函数关系式为_________________。123xyk=23xy21、在下列函数中，x是自变量，y是因变量，那些是一次函数？那些是正比例函数？y=2xy=－3x+1y=x2xy52、某函数具有下列两条性质（1）它的图像是经过原点（0，0）的一条直线；（2）y的值随x值的增大而增大。请你举出一个满足上述条件的函数（用关系式表示）1、已知函数y=(a-1)x+a+1,当a满足时，它为一次函数；当a满足时，它为正比例函数。在解答下列各小题过程中，回顾用到了哪些知识点？a≠1a=-1定义:函数y=kx＋b(k、b为常数，k≠０)叫做一次函数。当b=０时，函数y=kx(k≠０)叫做正比例函数。2、已知正比例函数y=kx，当x=-2时，y=6，则比例系数k=___-33、点P（2，-3）在函数y=kx+1的图象上，则k=。-2小结:已知一次函数的自变量和函数的一对对应值,可以求得一个字母系数的值.点在函数图象上，则点的坐标一定满足函数解析式。4、在如图所示平面直角坐标系中,点A的坐标为,点B的坐标为;直线AB的解析式是.yxo121AB一:回顾与总结(0,1)(2,0)y=-0.5x+1求解函数解析式的重要方法:_____________待定系数法待定系数法解：设y关于x的函数解析式为y=kx+b把A（1，1），B（-2，7）的坐标分别代入y=kx+b得：1=k+b7=-2k+b解这个方程组，得k=-2b=3∴y关于x的函数解析式为y=-2x+3设代解写已知一次函数的图象经过点A（1，1），B（-2，7），求这个一次函数的解析式。问题:(k≠0)同类变式一1、已知y-6与x+2成正比例，且当x＝3时，y＝－4；求y关于x的函数解析式。整体思想的运用2、某产品每件成本10元，试销阶段每件产品的销售价x（元）与产品的日销售量y（件）之间的关系如下表：若日销售量y是销售价x的一次函数．①求出日销售量y(件)与销售价x(元)的函数关系式②当销售价定为30元时，每日的销售量是多少?同类变式二x（元）152025…y（件）252015…msO2462846ABL3、如图,线段AL表示弹簧的长度s(cm)与所挂物体的质量m(kg)之间的关系的图象,请结合图象回答下列问题:(1):问题中的两个变量s与m之间是不是一次函数关系?(2):s与m之间的函数关系是________________;(3):由图知弹簧的原长是____cm.(4):当所挂物体的质量为3kg时,弹簧的长度s=___cm.(kg)(cm)是s=0.5m+67.5归纳:运用一次函数模型解决实际问题的基本步骤是：6根据图象判断函数的类型用待定系数法求出函数解析式解决有关函数的实际问题同类变式三(0≤m≤6)1.已知直线y=-2x+4,它与x轴的交点为A,与y轴的交点为B.(1).求A,B两点的坐标.(2).求∆AOB的面积.(O为坐标原点)2.已知某一次函数的图象经过(3,4),(-2,0)两点,试求这个一次函数的解析式.3.已知y是关于x的一次函数，这个函数的图象经过A（0，-8），B（1，2）两点，求当1