3三角函数的计算VIP免费

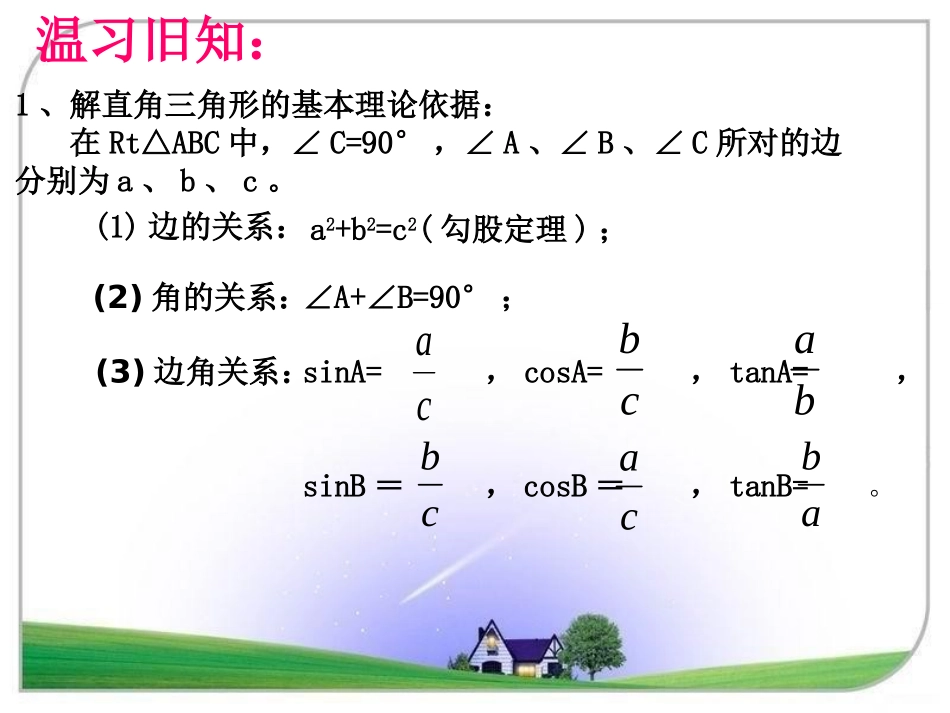
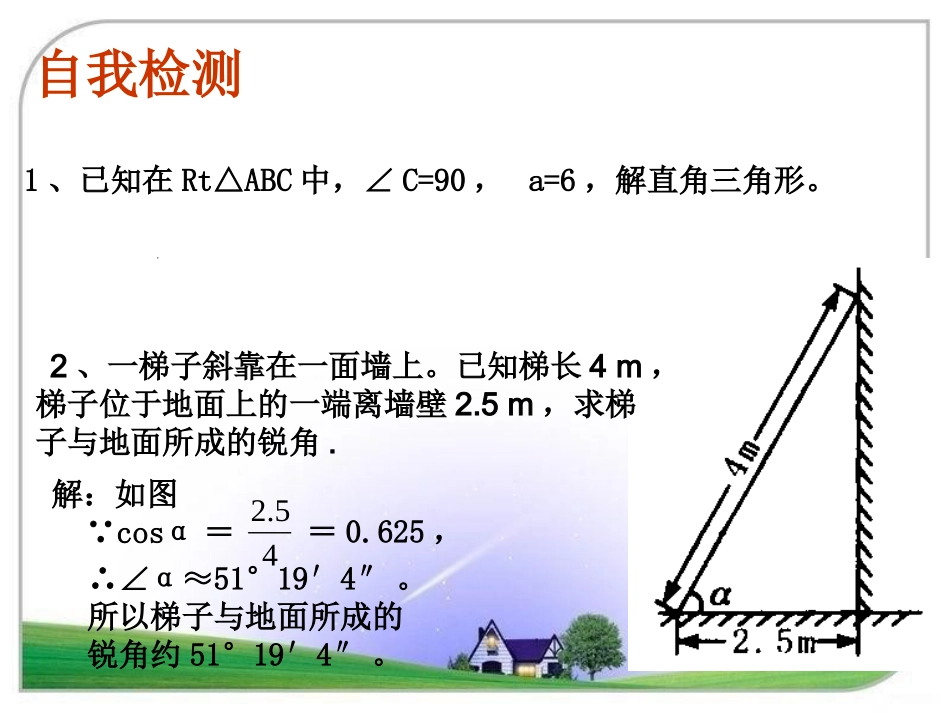
1、解直角三角形的基本理论依据：在Rt△ABC中，∠C=90°，∠A、∠B、∠C所对的边分别为a、b、c。(1)边的关系：a2+b2=c2(勾股定理)；(2)角的关系：∠A+∠B=90°；(3)边角关系：sinA=，cosA=，tanA=，sinB＝，cosB＝，tanB=。温习旧知：cbcabacbcaab45.21、已知在Rt△ABC中，∠C=90，a=6，解直角三角形。2、一梯子斜靠在一面墙上。已知梯长4m，梯子位于地面上的一端离墙壁2.5m，求梯子与地面所成的锐角.∴∠α≈51°19′4″。所以梯子与地面所成的锐角约51°19′4″。自我检测＝0.625，解：如图∵cosα＝如图,当登山缆车的吊箱经过点A到达点B时,它走过了200m.已知缆车行驶的路线与水平面的夹角为∠α=160,那么缆车垂直上升的距离是多少?在Rt△ABC中,BC=ABsin16°当缆车继续从点B到达点D时,它又走过了200m.缆车由点B到点D的行驶路线与水平面的夹角为∠β=420,由此你还能计算什么?随堂练习1.1.一辆汽车沿着一山坡行驶了一辆汽车沿着一山坡行驶了150150米，其铅直高度上升了米，其铅直高度上升了2525米，求山米，求山坡与水平面所成锐角的大小坡与水平面所成锐角的大小..解：如图，在RtABC△中，AC＝6.3cm，BC=9.8cm∴tanB=≈0.6429∴∠B≈因此，射线与皮肤的夹角约为。3144323144328.93.6BCAC解：∵tan∠ACD=≈0.5208∴∠ACD≈27.5°∴∠ACB＝∠ACD≈2×27.5°＝55°2.1910CDAD解决问题4、一个人由山底爬到山顶,需先爬400的山坡300m,再爬300的山坡100m,求山高(结果精确到0.01m).解：如图，根据题意，可知BC=300m，BA=100m，∠C=40°，∠ABF=30°.在RtCBD△中，BD=BCsin40°≈300×0.6428=192.8(m)在RtABF△中，AF=ABsin30°=100×=50(m).21所以山高AE=AF+BD＝192.8+50＝242.8(m).3.求图中避雷针的长度(结果精确到0.01m).解：如图，根据题意，可知AB=20m，∠CAB=50°，∠DAB=56°在RtDBA△中，DB=ABtan56°≈20×1.4826=29.652(m)；在RtCBA△中，CB=ABtan50°≈20×1.1918=23.836(m)所以避雷针的长度DC=DB-CB＝29.652-23.836≈5.82(m).通过这节课的学习，你有哪些收获？如图，某地夏日一天中午，太阳光线与地面成80°角，房屋朝南的窗户高AB=1.8m，要在窗户外面上方安装一个水平挡板AC，使光线恰好不能直射室内，求挡板AC的宽度.(结果精确到0.01m)活动与探究解：因为tan80°＝ACAB所以AC＝≈＝0.317≈0.32(m).80tanAB671.58.1所以水平挡板AC的宽度应为0.32米.