1.共点力作用下物体的平衡VIP专享VIP免费

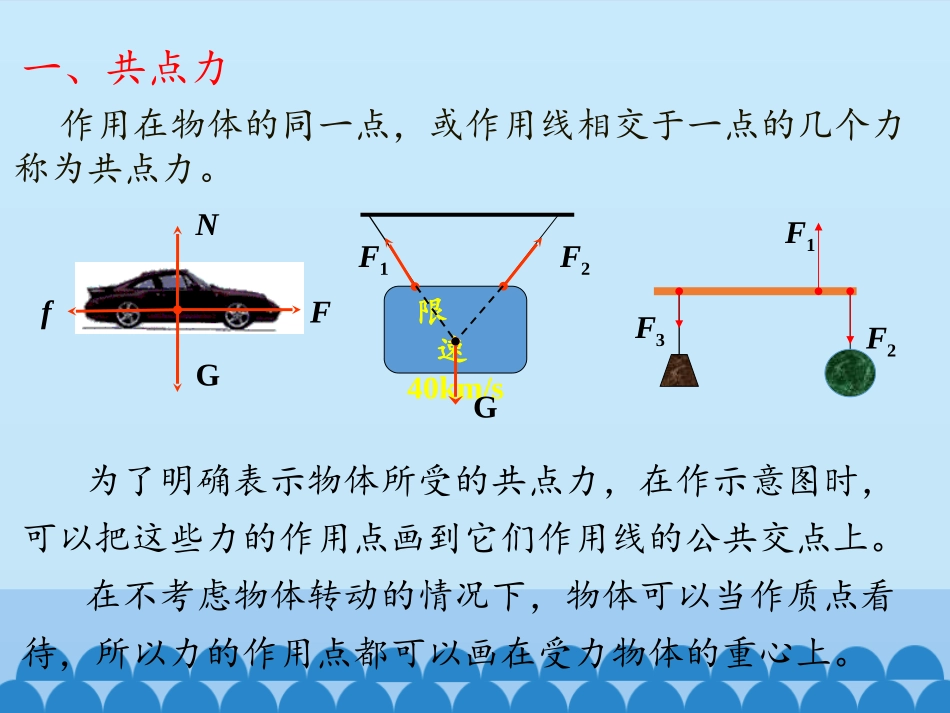
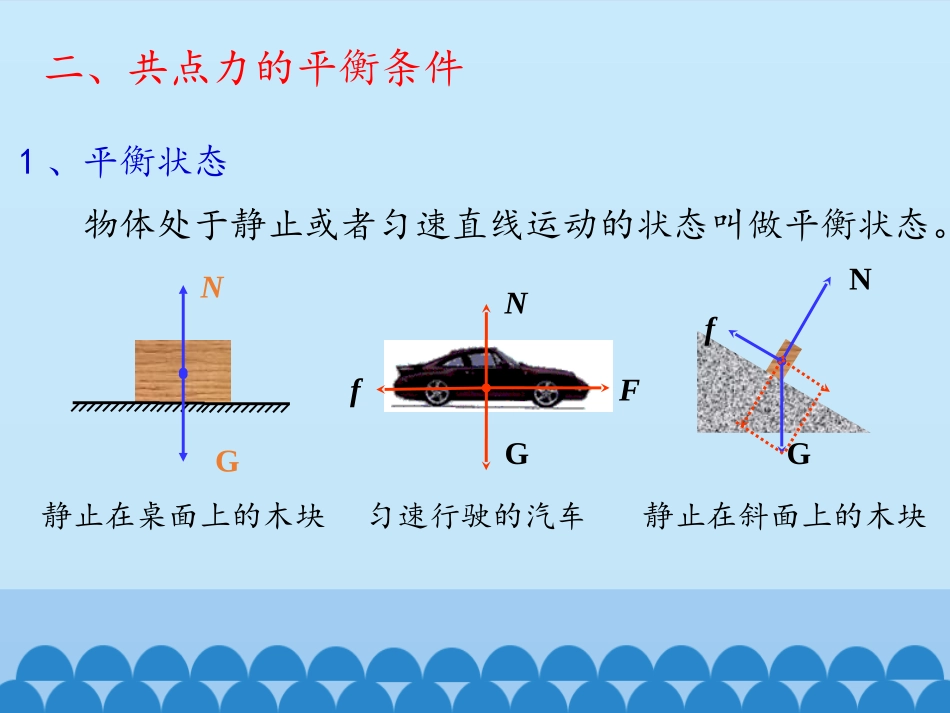
第一节共点力作用下物体的平衡限速40km/s作用在物体的同一点，或作用线相交于一点的几个力称为共点力。限速40km/sGF2F1F1F2F3FfNG为了明确表示物体所受的共点力，在作示意图时，可以把这些力的作用点画到它们作用线的公共交点上。在不考虑物体转动的情况下，物体可以当作质点看待，所以力的作用点都可以画在受力物体的重心上。一、共点力1、平衡状态物体处于静止或者匀速直线运动的状态叫做平衡状态。NG静止在桌面上的木块FfNG匀速行驶的汽车GNf静止在斜面上的木块二、共点力的平衡条件2、平衡的种类注：如果物体缓慢移动则称为准静态。（2）动平衡：物体保持匀速直线运动状态。（1）静平衡：物体保持静止状态3、平衡状态的运动学特征：V=0或V不变，即：a=0注意：保持静止和瞬时速度为0不同4、力的平衡条件：F合=0，或Fx合=0Fy合=0三、共点力作用下物体的平衡1、二力平衡条件：F合=0两力大小相等、方向相反，而且作用在同一物体、同一直线上.NG静止在桌面上的木块2、三力平衡条件：（1）设计实验方案方案1：弹簧秤两只，200g钩码两只，木板、白纸、图钉等，在竖直面内完成；〔实验探究〕方案2：弹簧秤三只，细线三根，木板、白纸、图钉等，在水平面内完成；（2）实验探究时要注意的几个问题：①用图钉将白纸固定在木板上②弹簧秤拉力方向要与弹簧伸长方向一致③结点尽可能在白纸的中央，以便于作图④由结点、三个细绳套端点确定三个力的方向时，视线要与木板垂直⑤作图时要用同一标度，标度大小要合适F1F3F2231FF（3）实验结论：F合=0任意两个力的合力与第三个力大小相等，方向相反，作用在同一直线上3、多力平衡条件：F合=0任意一个力都与其余各力的合力大小相等，方向相反，作用在同一直线上F23例1：如图所示，一个重为G的圆球，被一段细绳在竖直光滑墙上，绳与竖直墙的夹角为α，则绳子的拉力和墙壁对球的弹力各是多少？αFFNGFFNGF合αα解法一：合成法F=F合=G/cosαFN=GtanαFFNGF2ααF1拓展：若再减小绳长L，上述二力大小将如何变化？解法二：分解法F=F合=F2=G/cosαFN=F1=Gtanα例1：如图所示，一个重为G的圆球，被一段细绳挂在竖直光滑墙上，绳与竖直墙的夹角为α，则绳子的拉力和墙壁对球的弹力各是多少？FFNFyααFxGxy解法三：正交分解法X：FN-Fsinα=0Y：Fcosα-G=0解得：F=G/cosαFN=Gtanα——当物体处于平衡状态时，它所受的某一个力与它受的其余的力的合力等值反向。1、正确选取研究对象2、隔离物体，分析物体的受力，画出受力图3、根据作用效果，准确进行力的分解（或力的合成）4、根据平衡条件，列方程求解共点力的平衡解题方法小结重要推论此方法是力学解题中应用最普遍的方法，应注意学习。⑴共点力作用下物体的平衡条件是：F合=0；⑵在建立直角坐标系时，要考虑尽量减少力的分解。正交分解法把矢量运算转化成标量运算，极大的降低了数学应用的难度。再次认识正交分解法①选择研究对象：处于平衡状态下的物体；②对研究对象进行受力分析，画好受力图；③建立直角坐标系（原则是尽量减少力的分解）；④根据平衡条件布列方程⑤解方程(组)，必要时验证结论。0F00yxFF正交分解法解平衡问题的一般思维程序为AF160°F1FNGFyxθF1FNGFyxθ例2：物体A在水平力F1=400N的作用下，沿倾角θ=60°的斜面匀速下滑，如图所示。物体A受的重力G=400N，求斜面对物体A的支持力和A与斜面间的动摩擦因数μ.F1FNGFyxθ解：x:Gsinθ-F1cosθ-F＝0y:FN-Gcosθ-F1sinθ＝0F=μFN联立求解得：F=146.4Nμ=0.2683例2：物体A在水平力F1=400N的作用下，沿倾角θ=60°的斜面匀速下滑，如图所示。物体A受的重力G=400N，求斜面对物体A的支持力和A与斜面间的动摩擦因数μ.1.如图所示，质量为1kg的物体静止在倾角为30o的固定斜面上，则该物体受到的斜面的支持力和摩擦力分别为多大？30o解：对物体受力分析如图GNf得：xy课堂练习cos308.66NNmgsin305Nfmg1、下列说法正确的是()A．竖直上抛物体达最高点时，物体处于平衡状态B．电梯匀速上升时，电梯中的人处于平衡状态C．竖直弹簧上端固定，下端挂一个重物，平衡后用力F将它再往下拉一段距离后突然撤去力F，重...