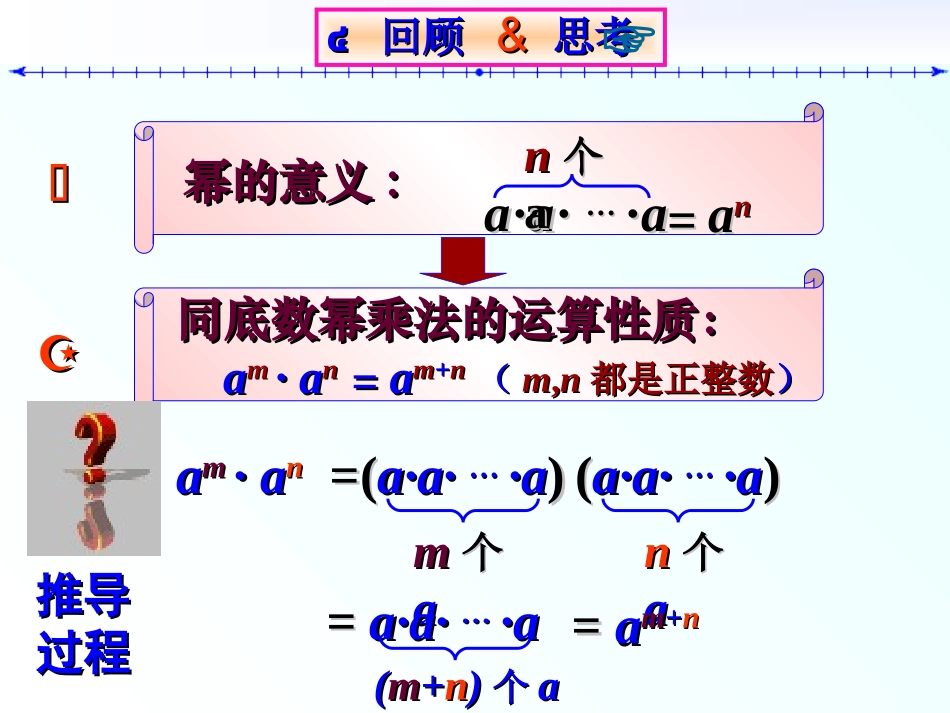
回顾与思考๔๔回顾回顾&&思考思考☞aamm·a·ann((a·a·a·a·……·a·a))nn个个aa==((a·a·a·a·……·a·a))mm个个aa==a·a·a·a·……·a·a((mm++nn))个个aa==aamm++nn幂的意义幂的意义::aa··aa··……··aann个个aaaann==同底数幂乘法的运算性质:同底数幂乘法的运算性质:aamm·a·ann==aamm++nn((mm,,nn都是正整数都是正整数))推导推导过程过程做一做做一做做一做计算下列各式,并说明理由计算下列各式,并说明理由..(1)(1)(6(622))44;;(2)(2)(a(a22))33;;(3)(3)(a(amm))22;;(4)(4)(a(amm))nn..解:解:(1)(1)(6(622))44(2)(2)(a(a22))33(3)(3)(a(amm))22=6=622··6622··6622··6622=6=62+2+2+22+2+2+2=6=688=a=a22·a·a22·a·a22=a=a2+2+22+2+2=a=a66=a=amm·a·amm=a=am+mm+m(4)(4)((aamm))nn==aamm··aamm··……··aamm个个aamm=a=am+m+m+m+……+m+m=a=amnmn((幂的意义)幂的意义)((同底数幂的乘法性质)同底数幂的乘法性质)((乘法的意义)乘法的意义)猜想猜想===6=622××44;;(6(622))44=a=a22××33;;(a(a22))33=a=a2m2m;;(a(amm))22aamnmn证证明明nn个个mmnn(a(amm))nn=a=amnmn(m,n(m,n都是正整数都是正整数))底数底数,,指数指数..幂的乘方,幂的乘方,幂的乘方幂的乘方法则法则不变不变相乘相乘例题解析【【例例11】】计算:计算:(1)(1)(10(1022))33;;(2)(2)(b(b55))55;;(3)(3)(a(ann))33;;(4)(4)-(x(x22))mm;;(5)(5)(y(y22))33·y·y;;(6)(6)2(a2(a22))66--(a(a33))44..(6)(6)2(a2(a22))66–(a–(a33))44=10=1022××33=10=1066;;(1)(1)(10(1022))33解:解:(2)(2)(b(b55))55=b=b55××55=b=b2525;;(3)(3)(a(ann))33=a=ann××33=a=a3n3n;;(4)(4)-(x(x22))mm==-xx22××mm==-xx2m2m;;(5)(5)(y(y22))33·y·y=y=y22××33·y·y=y=y66·y·y=2a=2a22××66-aa33××44=2a=2a1212-aa1212=a=a1212..=y=y77;;阅读阅读体验体验☞随堂练习:1、计算:naxxa232435233))(4())(3()()2()10)(1((5)(am)4(6)(x4)3·(x2)8(7)(a2)3·(a3)4(8)(am+3)2(9)[(x-3y)m]3(10)9m·27n注注11:幂的底数和指数不仅仅是单独字母:幂的底数和指数不仅仅是单独字母或数字,也可以是某个单项式和多项式或数字,也可以是某个单项式和多项式..下列各式是真是假:下列各式是真是假:(1)(a5)2=a7(2)a5·a2=a10(3)(x3)3=x6(4)x3m+1=(x3)m+1(5)a6·a4=a24(6)4m·4n=22(m+n)注注22:幂的乘方法则与同底数幂的乘法法则的异:幂的乘方法则与同底数幂的乘法法则的异同同).,()(都是正整数nmaamnnm).,(都是正整数nmaaanmnm注注33::多重乘方可以重复运用上述幂的多重乘方可以重复运用上述幂的乘方法则乘方法则..[(am)n]p=(amn)p=amnp注注44::幂的乘方公式还可逆用幂的乘方公式还可逆用..amn=(am)n=(an)m..5,3.223的值求已知:例nmnmaaa解:∵am=3,an=5∴a3m+2n=a3m·a2n=(am)3·(an)2=33×52=675.例例33计算计算(x-y)(x-y)mm(y-x)(y-x)2m2m+(y-x)+(y-x)3m3m..解:原式=(x-y)m(x-y)2m+(y-x)3m=(x-y)3m+(y-x)3m0m为奇数=2(x-y)3mm为偶数139.4xx解方程:例本节课你的收获是什么?幂幂的的意意义义幂幂的的意意义义积的乘方的运算性质:积的乘方的运算性质:((aamm))nn==aamnmn((m,nm,n都是正整数都是正整数))..同底数幂乘法的运算性质:同底数幂乘法的运算性质:aamm·a·ann==aamnmn((m,nm,n都是正整数都是正整数))底数不变,底数不变,指数相加指数相加..底数底数,,指数指数..相乘相乘不变不变