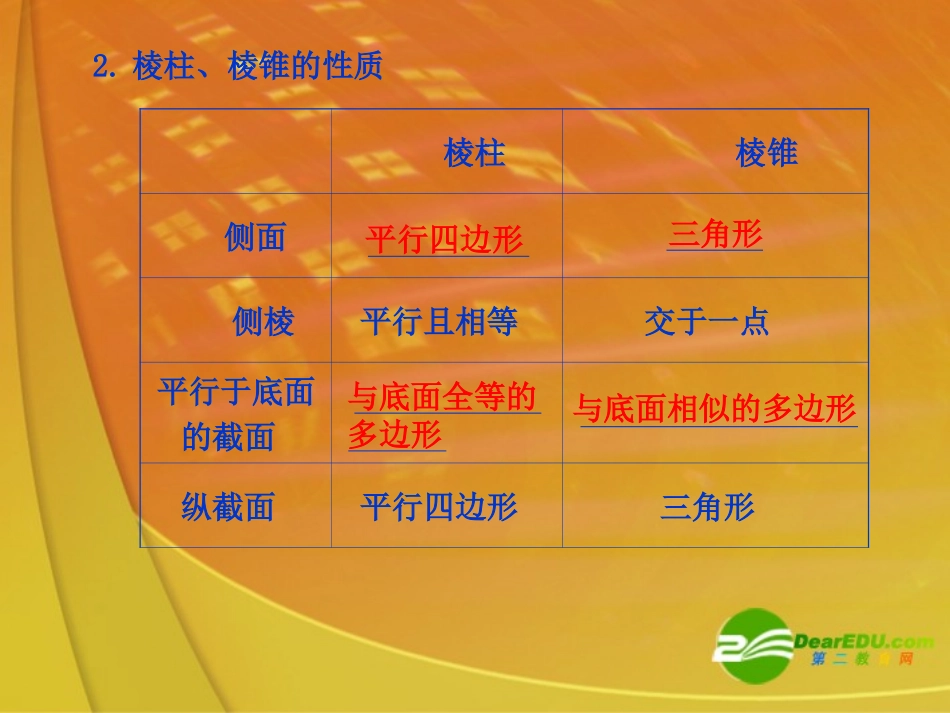
§9.5棱柱、棱锥的概念和性质基础知识自主学习要点梳理1.棱柱、棱锥的定义棱柱棱锥定义如果一个多面体有两个面互相,而其余每相邻两个面的交线互相,这样的多面体叫做棱柱如果一个多面体有一个面是,其余各面是的三角形,这样的几何体叫做棱锥平行平行多边形有一个公共顶点底面侧面其余各面侧棱顶点高两个侧面的公共边互相平行的面侧面与底面的公共顶点各侧面的公共顶点两个底面所在平面的公垂线段顶点到底面所在平面的垂线段多边形2.棱柱、棱锥的性质棱柱棱锥侧面侧棱平行且相等交于一点平行于底面的截面纵截面平行四边形三角形平行四边形三角形与底面全等的多边形与底面相似的多边形3.四棱柱的一些常用性质(1)平行六面体的四条对角线且在;(2)直棱柱的与高相等,直棱柱的及过的截面都是矩形,直棱柱的侧面与垂直;(3)正四棱柱与正方体的底面都是,正方体的侧面和底面都是;(4)长方体的等于同一个顶点上三条棱长的.交于一点该点互相平分侧棱长侧面不相邻两条侧棱底面正方形正方形一条对角线长的平方平方和若长方体的一条对角线与过同一个顶点的三条棱所成角分别为α、β、γ,则cos2α+cos2β+cos2γ=;若长方体的一条对角线与过同一个顶点的三个面所成角分别为α、β、γ,则cos2α+cos2β+cos2γ=.124.正棱锥是棱锥的特殊情形,是棱锥的主要研究对象(1)定义:底面是,并且顶点在底面上的射影是底面的,这样的棱锥叫做.(2)性质:①侧面是,与底面所成二面角均;②侧棱均,侧棱与底面所成的角均;③平行于底面的截面也是;纵截面是;④正棱锥中的基本元素:侧棱、斜高、高、底面外接圆半径、底面内切圆半径.正多边形中心正棱锥全等的等腰三角形相等相等相等正多边形等腰三角形5.体积公式(1)柱体体积公式为V=,其中为底面面积,为高;(2)锥体体积公式为V=,其中为底面面积,为高.6.侧面积与全面积(1)棱柱的侧面积是各侧面,直棱柱的侧面积是底面周长与;棱锥的侧面积是各侧面,正棱锥的侧面积是底面周长与.(2)全面积等于与之和,即S全=+.ShhSShSh31面积之和高之积面积之和斜高积的一半侧面积S侧S底底面积基础自测1.以下命题中正确的是()A.有两个面是对应边平行的全等多边形,其他面都是平行四边形的多面体是棱柱B.有一个面是多边形,其他面都是三角形的多面体是棱锥C.有三个侧面是矩形的棱柱是直棱柱D.长方体一定是正四棱柱C2.棱柱成为直棱柱的一个必要但不充分条件是()A.棱柱有一条侧棱与底面垂直B.棱柱有一条侧棱与底面的两条边垂直C.棱柱有一个侧面是矩形,且与底面垂直D.棱柱有两个侧面是矩形,且与底面垂直B3.已知长方体的全面积为11,十二条棱长度之和为24,则这个长方体的一条对角线长为()6.D5.C14.B32.AC4.(2009·陕西)若正方体的棱长为2,则以该正方体各个面的中心为顶点的凸多面体的体积为()解析由题意可知,此几何体是由同底面的两个正四棱锥组成的,底面正方形的边长为1,每一个正四棱锥的高为,所以32.D33.C32.B62.A22.32221312VB5.若一个正三棱柱的高为1,体积为2,则一条侧棱到与它相对的面之间的距离为()解析由体积公式V=Sh可得底面积为若设底面三角形的边长为a,则有所以a=2,故侧棱到相对面的距离为36.D3.C2.B1.A,32hVS,32432a2.623aD题型一棱柱、棱锥的概念和性质【例1】如果四棱锥的四条侧棱长都相等,就称它为“等腰四棱锥”,四条侧棱称为它的腰,以下5个命题中:①等腰四棱锥的腰与底面所成的角都相等;②等腰四棱锥的侧面与底面所成的二面角都相等或互补;③底面四边形存在外接圆的四棱锥是等腰四棱锥;④底面是正方形的四棱锥是等腰四棱锥;⑤等腰四棱锥的各顶点必在同一球面上.其中真命题为(写出所有真命题的序号).思维启迪结合“等腰四棱锥”的概念,逐一进行判断.解析①真.因为“等腰四棱锥”四条侧棱长都相等,故在底面上的射影长也相等,即顶点在底面上的射影是底面四边形外接圆的圆心,所以腰与底面所成的角都相等;②假.如当底面是矩形(不是正方形)时,且顶点在底面上的射影是底面中心时,这个四棱锥是“等腰四棱锥”,但它的侧面与底面所成的二面角显然不都相等或互补.故是假命题;③假.如当底...