2.2圆的对称性.2-圆的对称性1课件VIP免费

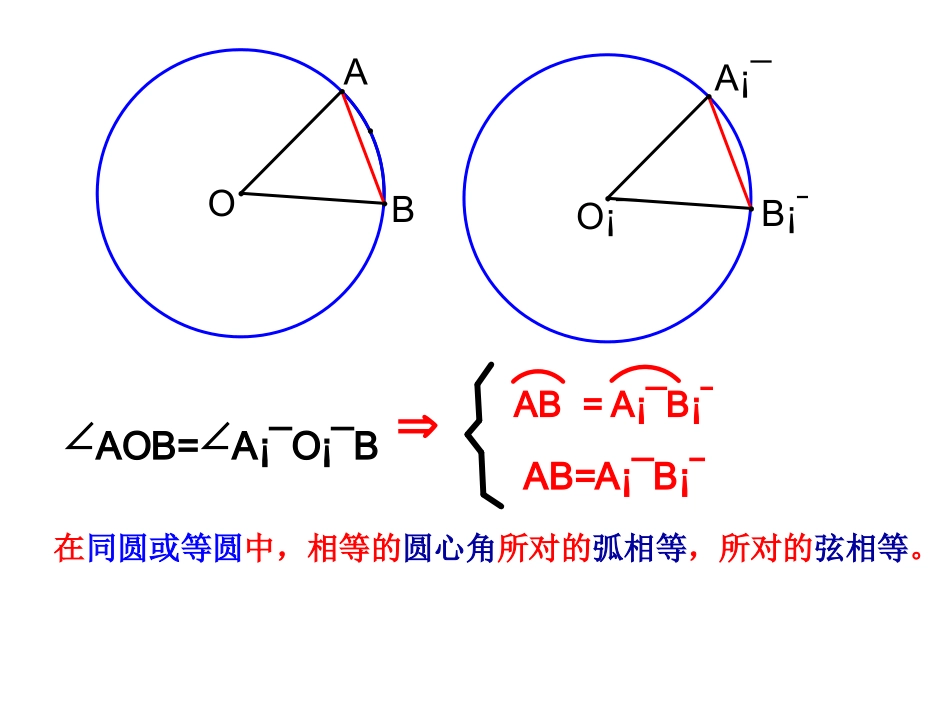
1、什么是中心对称图形？举例说明.把一个图形绕着某一个点旋转180∘，如果旋转后的图形能够和原来的图形互相重合，那么这个图形叫做中心对称图形。平行四边形、矩形、菱形、正方形复习提问：尝试与交流1.ÔÚÁ½ÕÅ͸Ã÷ֽƬÉÏ£¬·Ö±ð×÷°ë¾¶ÏàµÈµÄOºÍO¡¯2.ÔÚOºÍO¡¯ÖУ¬·Ö±ð×÷ÏàµÈµÄÔ²ÐĽÇAOB£¬A¡¯O¡¯B¡¯£¬Á¬½ÓAB£¬A¡¯B¡¯¡£3.½«Á½ÕÅ͸Ã÷ֽƬµþÔÚÒ»Æð£¬Ê¹OÓëOÖغϡ£OO'ABA'B'动画演示B¡¯A¡¯BAO¡¯OAOB=A¡¯O¡¯B¡¯AB=A¡¯B¡¯AB=A¡¯B¡¯在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等。思考与探索：在同圆或等圆中，如果圆心角所对的弧相等，那么它们所对的弦相等吗？这两个圆心角相等吗？为什么？B¡¯A¡¯BAO¡¯OAB=A¡¯B¡¯AOB=A¡¯O¡¯B¡¯AB=A¡¯B¡¯思考与探索：在同圆或等圆中，如果圆心角所对的弦相等，那么圆心角所对的弧相等吗？它们圆心角相等吗？为什么？B¡¯A¡¯BAO¡¯OAB=A¡¯B¡¯AB=A¡¯B¡¯AOB=A¡¯O¡¯B¡¯AB=A¡¯B¡¯AB=A¡¯B¡¯AOB=A¡¯O¡¯B¡¯AB=A¡¯B¡¯AB=A¡¯B¡¯AOB=A¡¯O¡¯B¡¯AB=A¡¯B¡¯AB=A¡¯B¡¯AOB=A¡¯O¡¯B¡¯1.2.3.在同圆或等圆中，如果两个圆心角，两条弧，两条弦中有一组量相等，那么它们所对应的其余各组都分别相等。(1)运用此性质的前提是:在同圆或等圆中.在同圆或等圆中，如果两个圆心角，两条弧，两条弦中有一组量相等，那么它们所对应的其余各组都分别相等。知一知一推二推二反思结论:(3)本知识是证明弦相等、弧相等的常用方法．(2)由一个条件,可以得到多个结论.DCBAO1µÄ»¡1µÄÔ²ÐĽÇnµÄ»¡nµÄÔ²ÐĽÇnµÄÔ²ÐĽǶÔ×ÅnµÄ»¡£¬nµÄ»¡¶Ô×ÅnµÄÔ²ÐĽǡ£Ô²ÐĽǵĶÈÊýÓëËüËù¶ÔµÄ»¡µÄ¶ÈÊýÏàµÈ¡£Àý1£ºÈçͼÔÚABCÖУ¬C=90£¬B=28£¬ÒÔCΪԲÐÄ£¬ÒÔCAΪ°ë¾¶µÄÔ²½»ABÓÚµãD£¬½»BCÓÚµãE£¬ÇóAD£¬DEµÄ¶ÈÊý¡£EDCBACBAO½â£ºABC=BAC¡ßAOC=BOCAC=BCABC=BAC2.如图,AB、AC、BC都是⊙O的弦，若∠AOC=∠BOC,则∠ABC与∠BAC相等吗？为什么？OFEDCBA︵3.已知：如图，AB是⊙O的直径，点C、D在⊙O上，CEAB⊥于E，DFAB⊥于F，且AE=BF，AC与BD相等吗？为什么？⌒⌒⌒⌒练习：1.Èçͼ£¬ÔÚOÖУ¬AC=BD£¬AOB=50£¬ÇóCODµÄ¶ÈÊý¡£2.Èçͼ£¬ÔÚOÖУ¬AB=AC£¬A=40£¬ÇóABCµÄ¶ÈÊý¡£CBAODCBAODCBAOOECDBA1.如图，AB、CD是⊙O的直径，弦CEAB,CE∥的度数为40°.求∠AOC的度数.⌒⌒3.Èçͼ£¬ÔÚͬԲÖУ¬ÈôAOB=2COD£¬ÔòABÓë2CDµÄ´óС¹ØϵÊÇ£¨£©£¨A£©AB£¾2CD(B)AB£¼2CD(C)AB£½2CD(D)²»ÄÜÈ·¶¨DCBAOC4.ÔÚͬԲÖУ¬ÈôAB=2CD£¬ÔòABÓë2CDµÄ´óС¹ØϵÊÇ£¨£©£¨A£©AB£¾2CD(B)AB£¼2CD(C)AB£½2CD(D)²»ÄÜÈ·¶¨DCBAOB课后小结：1.圆是中心对称图形，圆心是它的对称中心。2.在同圆或等圆中，如果两个圆心角，两条弧，两条弦中有一组量相等，那么它们所对应的其余各组都分别相等。Ô²ÐĽǵĶÈÊýÓëËüËù¶ÔµÄ»¡µÄ¶ÈÊýÏàµÈ¡£3.