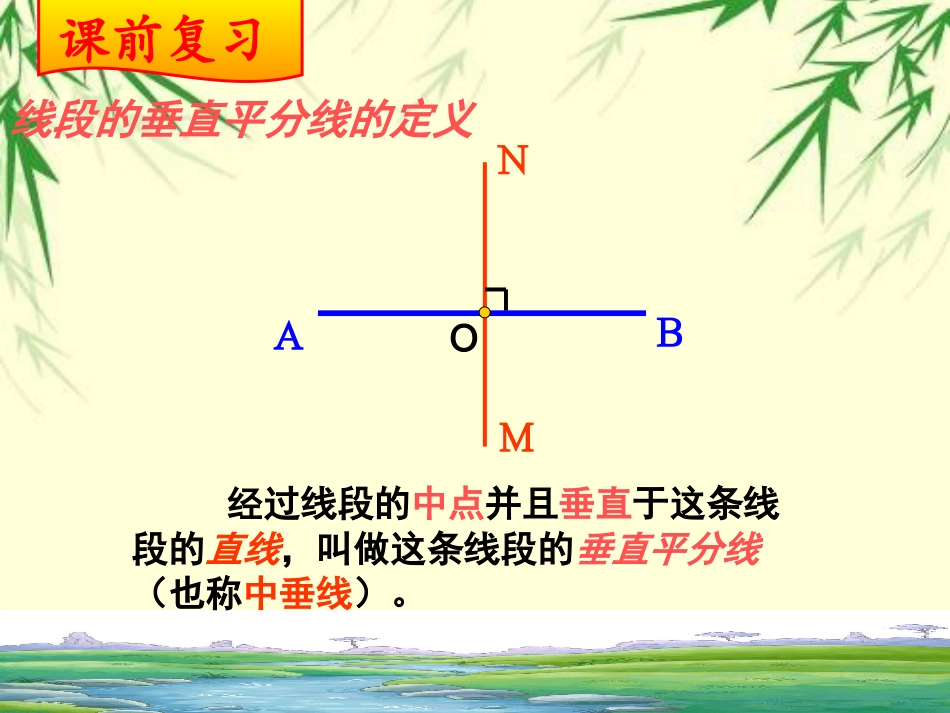
13.1.2线段的垂直平分线的性质课前复习1线段的垂直平分线的经过线段的中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线(也称中垂线)。经过线段的中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线(也称中垂线)。线段的垂直平分线的定义ABNMO课前复习线段AB的中垂线MN,垂足为C;在MN上任取一点P,连结PA、PB;量一量:PA、PB的长,你能发现什么?PMNCPA=PBP1A=P1B……由此你能得到什么规律?命题:线段垂直平分线上的点和这条线段两个端点的距离相等。画一画AB●P1命题:线段垂直平分线上的点和这条线段两个端点的距离相等。已知:如图,直线MNAB,⊥垂足为C,且AC=CB.点P在MN上.求证:PA=PB证明:∵MNAB⊥∴∠PCA=PCB∠在ΔPAC和ΔPBC中,AC=BC∠PCA=PCB∠PC=PC∴ΔPACΔPBC≌∴PA=PB证一证ABPMNC性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等。ABPMNCPA=PB点P在线段AB的垂直平分线上性质定理有何作用?可证明线段相等定理应用格式:∵AC=BC,MNAB,P⊥是MN上任意一点∴PA=PB(线段垂直平分线性质)线段垂直平分线性质1、如图,ADBC⊥,BD=DC,点C在AE的垂直平分线上,AB、AC、CE的长度有什么关系?AB+BD与DE有什么关系?AC=CEAB+BD=DEECDBAABPCPA=PB点P在线段AB的垂直平分线上(利用全等,仿照性质定理自己证明)反过来,如果PA=PB,那么点P是否在线段AB的垂直平分线上?换一换判定定理:与一条线段两个端点距离相等的点,在这条线段的垂直平分线上。判定定理有何作用?用途:判定一条直线是线段的中垂线2、如图,AB=AC,MB=MC,直线AM是线段BC的垂直平分线吗?ABCM(1)线段AB的垂直平分线上的所有点都满足“与点A、B的距离相等”这一条件吗?线段的垂直平分线可以看作是和线段两个端点距离相等的所有的点的集合想一想(2)满足“与A、B的距离相等”的所有点都在线段AB的垂直平分线上吗?尺规作图•经过直线外一点作这条直线的垂线。•已知:直线AB和AB外一点C•求作:AB的垂线,使它经过点C用一根木棒和一根弹性均匀的橡皮筋,做一个简易的“弓”,“箭”通过木棒中央的孔射出去,怎样才能保持射出去的方向与木棒垂直呢?只要AC=BC就可以了ABC为什么?在南安大道同侧,有两个小区A、B,为了便于两区的居民出行,县政府计划在公路边上修建一个公交汽车站,使得两个小区的居民到公交站的距离相等,公交站牌应选在何处?学以致用南安大道二、逆定理:与一条线段两个端点距离相等的点,在这条线段的垂直平分线上。线段的垂直平分线一、性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等。PA=PB点P在线段AB的垂直平分线上线段垂直平分线判定线段垂直平分线性质三、线段的垂直平分线的集合定义:线段的垂直平分线可以看作是和线段两个端点距离相等的所有点的集合