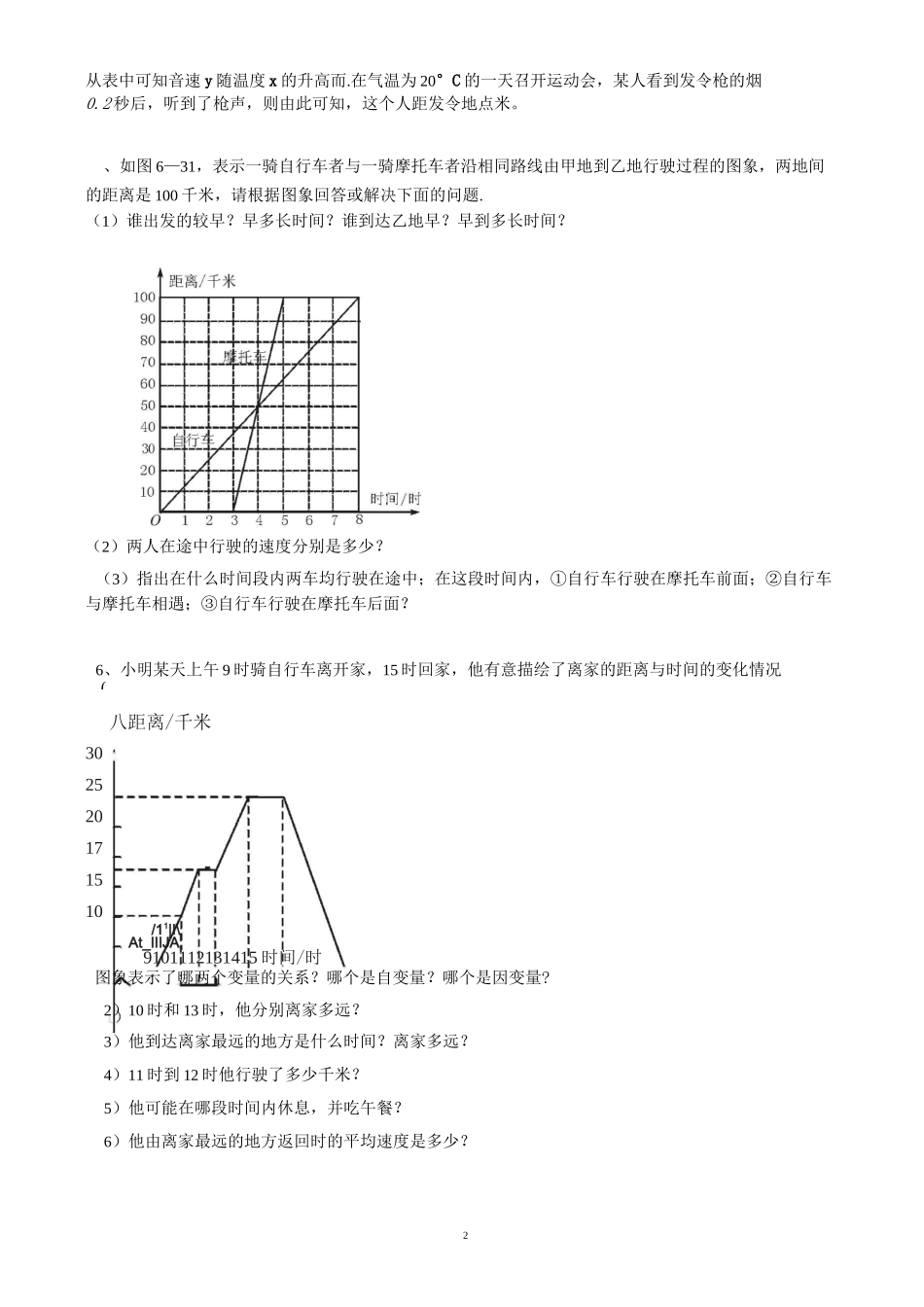
1变量之间的关系一、基础知识回顾:1.表示两个变量之间关系的方法有()、()、().2.图象法表示两个变量之间关系的特点是()3.用图象法表示两个变量之间关系时,通常用水平方向的数轴(横轴)上的点表示(),用竖直方向的数轴(纵轴)上的点表示().专题一、速度随时间的变化1、汽车速度与行驶时间之间的关系可以用图象来表示,下图中A、B、C、D四个图象,可以分别用一句话来描述:1)在某段时间里,速度先越来越快,接着越来越慢。()2)在某段时间里,汽车速度始终保持不变。()3)在某段时间里,汽车速度越来越快。()4)在某段时间里,汽车速度越来越慢。()2、李明骑车上学,一开始以某一速度行进,途中车子发生故障,只好停下修车,车修好后,因怕耽误时间,于是加快了车速.如用s表示李明离家的距离,t为时间.在下面给出的表示s与t的关系图6—41中,3、“龟兔赛跑”讲述了这样的故事:领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了一觉。当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点„„.用S1、S2分别表示乌龟和兔子所行的路程,t为时间,则下列图象中与故事情节相吻合的是()4、声音在空气中传播的速度y(米/秒)(简称音速)与气温x(°C)之间的关系如下:气温(xC)05101520音速y(米/秒)331334337340343速速B速度速度2(从表中可知音速y随温度x的升高而.在气温为20°C的一天召开运动会,某人看到发令枪的烟0.2秒后,听到了枪声,则由此可知,这个人距发令地点米。、如图6—31,表示一骑自行车者与一骑摩托车者沿相同路线由甲地到乙地行驶过程的图象,两地间的距离是100千米,请根据图象回答或解决下面的问题.(1)谁出发的较早?早多长时间?谁到达乙地早?早到多长时间?(2)两人在途中行驶的速度分别是多少?(3)指出在什么时间段内两车均行驶在途中;在这段时间内,①自行车行驶在摩托车前面;②自行车与摩托车相遇;③自行车行驶在摩托车后面?6、小明某天上午9时骑自行车离开家,15时回家,他有意描绘了离家的距离与时间的变化情况八距离/千米302520171510/11|I\At_IIIJA9101112131415时间/时图象表示了哪两个变量的关系?哪个是自变量?哪个是因变量?2)10时和13时,他分别离家多远?3)他到达离家最远的地方是什么时间?离家多远?4)11时到12时他行驶了多少千米?5)他可能在哪段时间内休息,并吃午餐?6)他由离家最远的地方返回时的平均速度是多少?0(A)TT牛T」T/r0r\J01(B)t0[(C)t0(D)t大约在()时,大山的体温最;(大山的体温在降低的时段是3专题二、温度与时间的关系1、夏天,一杯热水越来越凉,图中可表示这杯水的水温T与时间t的函数关系的是(、气温与海拔高度有关,一般情况下,每升高1km,气温下降6°C.某山地面温度为28°C,请写出气温t(°C)与高度h(km)之间的关系式:.(2)大约什么时间其体温最低?最低体温是多少?(3)在什么时间内其体温在降低?(4)在什么时间内其体温在升高?(5)A、B两点分别表示什么?(6)从大体上说说体温在24小时内的变化情况.(大约在时,大山的体温最高,这时最高体温是底,最低体温是大山的体温在升高的时段是4、大图象能大致表示水的最大深度和时间之间的关系?4专题三、高度(深度)与时间的变化、如图是某蓄水池的横断面示意图,分深水区和浅水区,如果这个蓄水池以固定的流量注水,下面哪个2、如图:向放在水槽底部的烧杯注水(流量一定)注满烧杯后,继续注水,直至注满水槽,水槽中水面上升高度与注水时间之间的关系大致是下列图象中的()3、气温随高度而变化的过程中,是自变量,因变量、一圆锥的底面半径是,当圆锥的高由变到时,圆锥的体积由cm3变到cm3、弹簧的长度与所挂物体的质量的关系如图一所示,由图可知不挂重物时弹簧的长度为5、一年中,每天日照(从日出到日落)日到年月日的日照时间6、.在弹性限度内,某弹簧伸长的总长度y(cm)与所挂重物质量x(g)之间的关系如下表.重物质量x(g)012345弹簧伸长的总长度y(cm)88+0.28+0.48+0.68+0.88+1.0(1)上表反映了和两个量之间的关系⑵关于y与x之间的关系式是.7、A4BC的底边BC=8cm,当BC边上的高线从小到大变化时,AABC的面积也随...