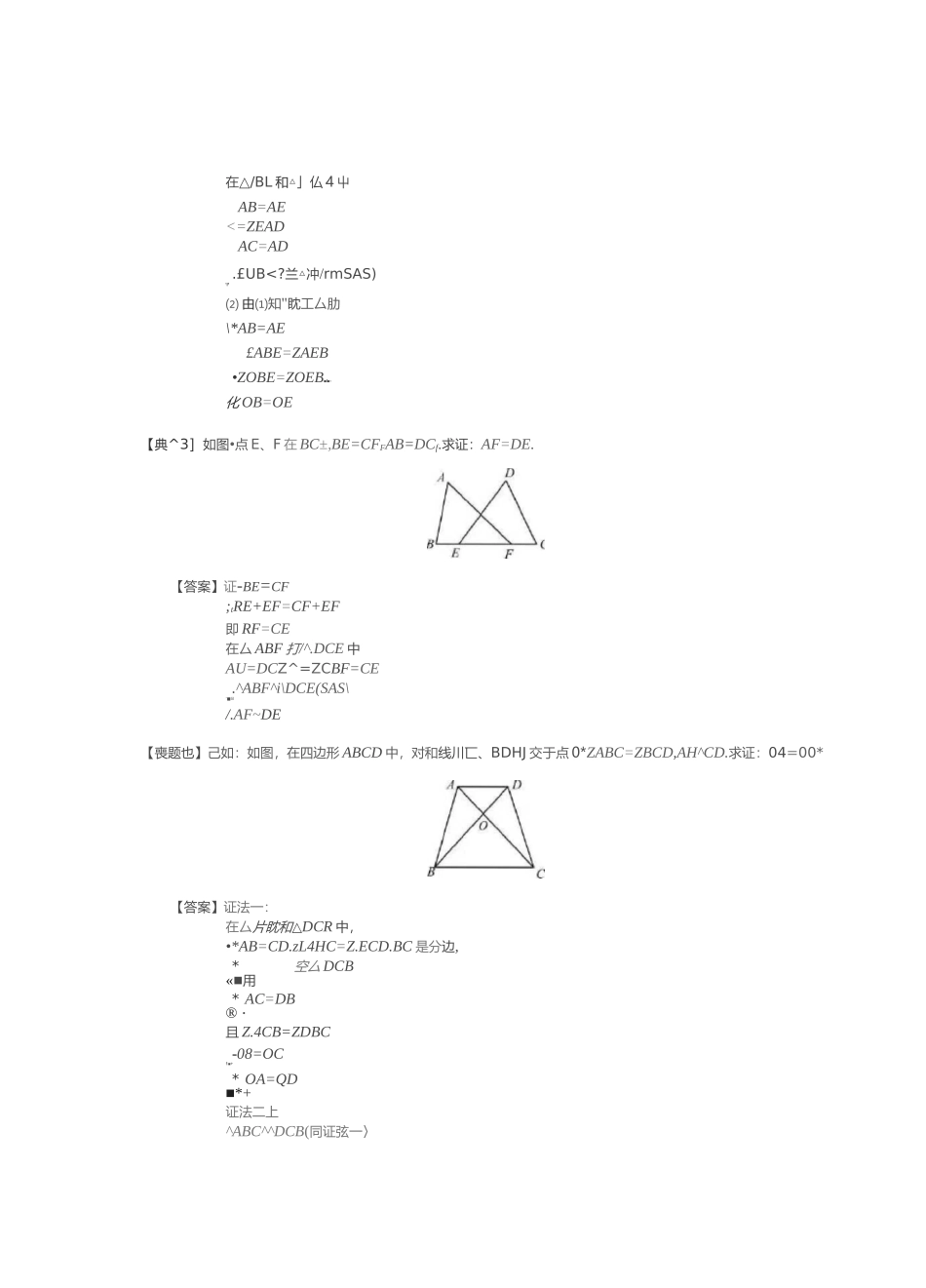
全等三角形典型50例模型及答案BaDD灵撲块一全縛基本模型全爭三狎啊50例【业理1】证明:两曇等三甫形的对臧建的角平分鏡相尊.【需案】已和:△加?厂空△用孑L,AD7-分疋加匸凭肌'于D,才以平分止/机"宜扩<7于/.求证:AD=A'[y.iiE明:»;△沖iff竺扛卅B'U,/,^BAC=^B'A'C,在△冲別)和△序日刖中.\^RAD=^ffA'iyx/mzfi=zs*/.△.婕门竺pI:腥題2】如怪I,&dBE中*A13-AE,AD=AC,^BAD=ZEAC.B€,DE兗于点门一求证:⑴△朋C空AHED:⑵OB=QE,【答案】⑴丁邀射◎須;,ZBAC=^EAD■/.4D平分^BAC交用匸于门.ZHAD=丄£BAC=丄^afArC22X©平分ZS^c交护圧于Q=zs\ri>在△/BL和△」仏4屮AB=AE<=ZEADAC=AD.£UB【答案】⑴连结月「肚,则公ABC^^AFEt:tAC=AE^又丁。是CE的屮点tAD丄CT⑵/ID丄BF,BF//CE【典題6】如图'在血边形ABCDE中,ZS=ZE,ZC=ZPTBC=DE・求证:从f丄CD.M为CDip点+【答案】分别延长理佈°C交于点尸:分别延长交于点°*/.ABO-ZDCO又TAAOB=ZDOC,*J\AOB^/\DOC■-■'■*OA=OD*9',d【典麵】如图所示.AB=AFrRC=FE・的"F・DCE的屮点.⑴求证:加丄少;⑵连接RF后,还能得出什么结论?请你写出两个(不要求证明)・Z3=Z4»■同理:Z5=Z6在△"净和屮Z5=Z6/BC=EDZ3=Z4*APC5^^QDE{ASA)9'S'..Zl=・许二理CP二DQ.AP=AQ■B■丫CM=DM*加=QM加为等腔△丿尸。底边中点/.AM丄CD【典题7】如图•把长方形ABCD{AB=CD.AD=BC,ZA=ZABC=AC=^CDA=90°)ft纨甘D对析,使点C落在应U处,诸说明AE^CE.【答定】"EB二8ED.Z4=^C=90°rAB^CD^C'Dr*ACO£・AE=CE■■9•*0【典题盯将两个全等的直角三角形冲此和帥E按劉①方式摆派:K中二厶兀E=9F’ZJ=ZP=3^,点E落在初上,所在直线交M所在直线于点厂⑴求证;WF+EFf⑵若将图I屮的△礙绕总£按顺时封方向旄转肿.且共他糸件不变,请在图2屮画出变换肩的图形*并直接写出⑴中的结论是否仍然威屯⑶若将图1中的△览财绕点⑥按顒时针方向旋转角仪且妙慕他条件平变,如图3-你认为⑴中的结论还咸立吗?若成立,写出证明过程;若不成立,请写出此时用7、EF与DE之间的关爲井说明理由.【铮案](1)连结RF,•厶BED空氏吕CA,:.BE=RC.又丫出尸览公共边,+RtAffC^^RlA^EF*CF二EFAF+=AC=DE♦鼻■审■P4*■£■⑵成立⑶不成立,AF-EF=DE,连结*F’口⑴同理「RtABCFRLA5£THCF-EF,AF-EF—AC=DEC戈'模块二角平分线基本模型【典趨刀△肋C中.⑴如圏I*若如C的平分线过*C的中点D,错想畀£与彳&的关系并证明.⑵如图2,若^AC的平分线不过眈的中点D,而是与兀的垂直平分线交于点E,过£作EF丄垂足为F,猜想&尸、肋、「°C的关系并证明.证明:过。作DM丄A8『MrDN丄.4用于N,丁AD平分T二DM=DN,V"-W-AD+BD=CD△・ADMAtiDMACD.V*AM=ANSM=CN*AB=AC,*•TF*■;⑵猜想:2亦=仙-犹;证明:连结EP、ECtEfl:EG丄・4C交延长线于点G■/AE平分£BAC,EF丄AB,EG丄眉fF.:EF=EG,AF=AG:・DE4ft比平分BC,BE=CE,/,£\EBF旦HECGt/.BF=CG,.AB-AC=^F+BF{AG-CG)=2BF【典是10】切I图tA.^C的轴平分线AD.呢相交于点F,已知=⑴求厶PF的酸数;⑵说明F"=尸E的理由.ECCDMBaZ/iFE="AH+=—£CAB+-CBA=一(I別)”一EM)=枳尸偕案】⑴22D⑵过P作只讨丄眈于加,PN丄卫y连结PC"6RE匙"£的侑平分线,二户<7平分厶tCR,化P,W=PN’Z?OV=ZAUD+=ZJZfP+圧PHU4-Z8AD=SPE+APBC-60°+ZP^CaZPEN二ZEBC+£E