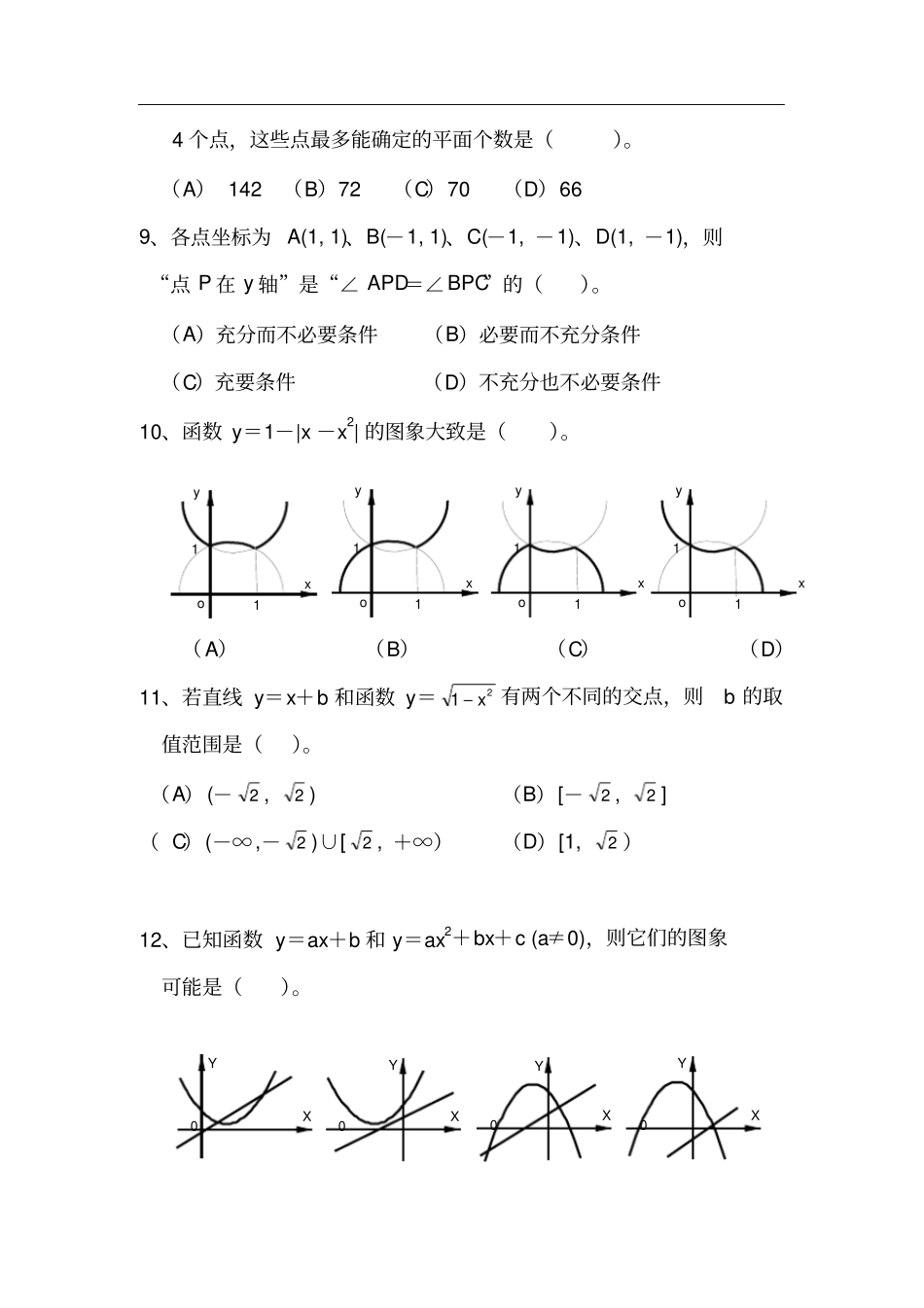
2018年上海市高考数学选择题常考考点专练151、平面α与平面β平行,它们之间的距离为d(d>0),直线a在平面α内,则在平面β内与直线a相距2d的直线有()。(A)一条(B)二条(C)无数条(D)一条也没有2、互不重合的三个平面可能把空间分成()部分。(A)4或9(B)6或8(C)4或6或8(D)4或6或7或83、若a,b是异面直线,aα,bβ,α∩β=c,那么c()。(A)同时与a,b相交(B)至少与a,b中一条相交(C)至多与a,b中一条相交(D)与a,b中一条相交,另一条平行4、直线a//平面M,直线bM,那么a//b是b//M的()条件。(A)充分不必要(B)必要而不充(C)充要(D)不充分也不必要5、和空间不共面的四个点距离相等的平面的个数是()。(A)7个(B)6个(C)4个(D)3个6、在长方体相交于一个顶点的三条棱上各取一个点,那么过这三点的截面一定是()。(A)三角形或四边形(B)锐角三角形(C)锐角三角形或钝角三角形(D)钝角三角形7、圆锥底面半径为r,母线长为l,且l>2r,M是底面圆周上任意一点,从M拉一条绳子绕侧面转一周再回到M,那么这条绳子的最短长度是()。(A)2πr(B)2l(C)2lsinlr(D)lcoslr8、α、β是互不重合的两个平面,在α内取5个点,在β内取4个点,这些点最多能确定的平面个数是()。(A)142(B)72(C)70(D)669、各点坐标为A(1,1)、B(-1,1)、C(-1,-1)、D(1,-1),则“点P在y轴”是“∠APD=∠BPC”的()。(A)充分而不必要条件(B)必要而不充分条件(C)充要条件(D)不充分也不必要条件10、函数y=1-|x-x2|的图象大致是()。(A)(B)(C)(D)11、若直线y=x+b和函数y=21x有两个不同的交点,则b的取值范围是()。(A)(-2,2)(B)[-2,2](C)(-∞,-2)∪[2,+∞)(D)[1,2)12、已知函数y=ax+b和y=ax2+bx+c(a≠0),则它们的图象可能是()。yxo11yxo11yxo11yxo11YX0YX0YX0YX0(A)(B)(C)(D)13.(本小题满分14分)已知在△ABC中,a,b,c分别为角A,B,C所对的边,tan(4C)23.(1)求角C的大小;(2)若43sinsinBA,试判断△ABC的形状,并说明理由.14.(本小题满分14分)如图,在正三棱柱111CBAABC中,点D在棱BC上,DCAD1,点E,F分别是1BB,11BA的中点.(1)求证:D为BC的中点;(2)求证://EF平面1ADC.(第16题)15(本小题满分14分)某校学生社团心理学研究小组在对学生上课注意力集中情况的调查研究中,发现其注意力指数p与听课时间t之间的关系满足如图所示的曲线.当]14,0(t时,曲线是二次函数图象的一部分,当]40,14[t时,曲线是函数835logxya(0a且1a)图象的一部分.根据专家研究,当注意力指数p大于80时听课效果最佳.(1)试求()pft的函数关系式;(2)老师在什么时段内安排核心内容能使得学生听课效果最佳?请说明理由.(第15题)AA1BCB1C1DEF81pO12144082t题号123456789101112答案BDBAABCBACDB13.(本题满分14分)解:(1)32)4tan(C,321tan1tanCC,3tanC⋯⋯⋯⋯⋯4分C0,3C.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯6分(2)43sinsinBA,又23sinCCBA2sinsinsin,由正弦定理得2cab⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯10分由余弦定理得abbaCabbac22222cos202ba,ba,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯12分又3C,ABC是正三角形.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯14分14.(本题满分14分)解:(1)正三棱柱111CBAABC,CC1平面ABC,又AD平面ABC,ADCC1,又DCAD1,111CCCDCAD平面11BBCC,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3分又正三棱柱111CBAABC,平面ABC平面11BBCC,ADBC,D为BC的中点.⋯⋯⋯6分(2)连接BA1,连接CA1交1AC于点G,连接DGA1B1C1FG矩形11ACCA,G为CA1的中点,又由(1)得D为BC的中点,△BCA1中,BADG1//⋯⋯⋯⋯⋯⋯⋯9分又点E,F分别是1BB,11BA的中点,△BBA11中,BAEF1//,DGEF//,⋯⋯⋯12分又EF平面1ADC,DG平面1ADC,//EF平面1ADC.⋯⋯⋯14分15.(本题满分14分)解:(1)]14,0(t时,设2()(12)82pftct(0c),将)81,14(代入得41c]14,0(t时,21()(12)824pftt⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2分]40,14[t时,将)81,14(代入835logxya,得31a⋯⋯⋯4分∴2131(2)82(014)4()log(5)83(1440)ttpfttt.⋯⋯⋯⋯⋯⋯⋯⋯⋯6分(2)]14,0(t时,21(12)82804t解得22122212t,∴]14,2212[t⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯9分]40,14[t时,8083)5(log31t解得325t,∴]32,14[t,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯12分∴]32,2212[t,即老师在]32,2212[t时段内安排核心内容能使得学生听课效果最佳.⋯14分