排列与排列数1PPT课件VIP免费

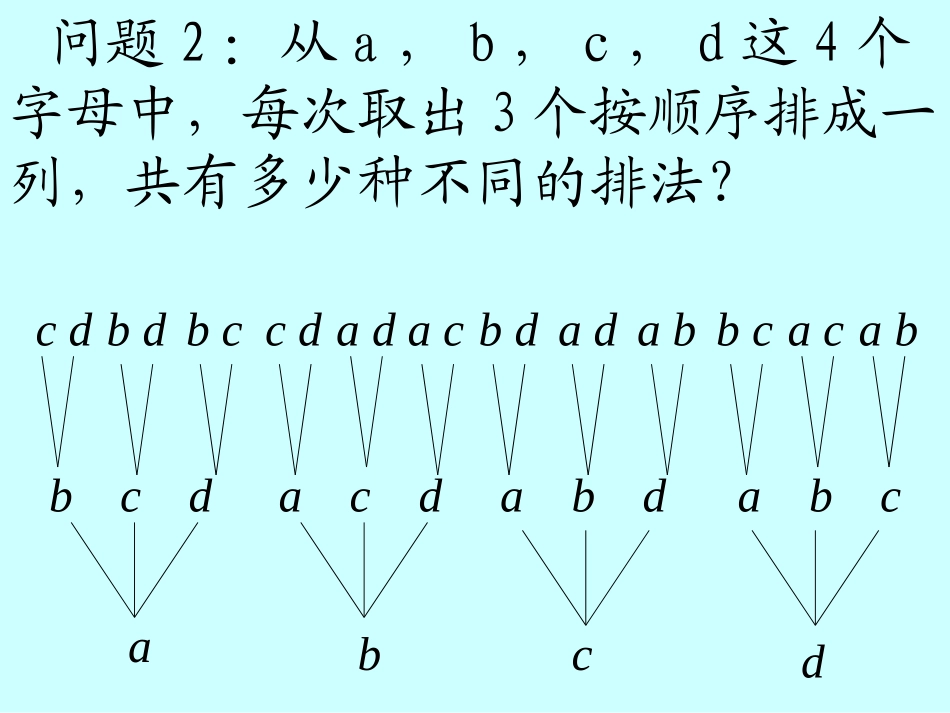
排列与排列数兆麟中学高二数学组问题1：从甲、乙、丙3名同学中选出2名参加某天的一项活动，其中1名同学参加上午的活动，1名同学参加下午的活动，有多少种不同的方法？问题1bdadabbcacabcdacadcdbdbcbacdbcdacdabdabc问题2：从a，b，c，d这4个字母中，每次取出3个按顺序排成一列，共有多少种不同的排法？所有的排列为：abcbaccabdababdbadcaddacacbbcacbadbaacdbcdcbddbcadbbdacdadcaadcbdccdbdcb一般地说，从n个不同元素中，任取m(m≤n)个元素，按照一定的顺序排成一列，叫做从n个不同元素中取出m个元素的一个排列。排列的定义中包含两个基本内容：一个是“取出元素”；二是“按照一定顺序排列”，“一定顺序”就是与位置有关，这也是判断一个问题是不是排列问题的重要标志。根据排列的定义，两个排列相同，且仅当两个排列的元素完全相同，而且元素的排列顺序也相同。下列问题是排列问题吗？（1）从1，2，3，4四个数字中，任选两个做加法，其结果有多少种不同的可能？（2）从1，2，3，4四个数字中，任选两个做除法，其结果有多少种不同的可能？（3）从1到10十个自然数中任取两个组成点的坐标，可得多少个不同的点的坐标？不是是是（4）平面上有5个点，任意三点不共线，这五点最多可确定多少条直线？可确定多少条射线？（5）10个学生排队照相，则不同的站法有多少种？是是不是从n个不同元素中取出m(m≤n)个元素的所有排列的个数，叫做从n个不同元素中取出m个元素的排列数，用符号表示。排列数公式Amn第1位第2位nn-1)1(2nnAn······第1位第2位第3位第m位)1()2()1(mnnnnAmnnn-m+1n-2n-1)2()1(nnnAnn•···•3•2•1)1()2()1(mnnnnAmnnAnn！排列数公式提示因为最大数为17，是17－4＋1＝14个数的积，∴n＝17，m＝14.3．排列数公式(1)乘积形式：Amn＝_________________________．(这里n，m∈N*且m≤n.)(2)阶乘形式：Amn＝n！（n－m）！.(n，m∈N*，且m≤n)(3)性质：Ann＝n！规定A0n＝__，0！＝1.n(n－1)(n－2)…(n－m＋1)1试一试：如果Amn＝17×16×15×…×5×4，则n＝________，m＝________．例1计算：.)3(;)2(;)1(66712812316AAAA336014151656789101112567891011126！=6×5×4×3×2×1=720练习：?)4(?)3(?24)2(140)1(163259694858598858483412nnnnnAAAAAAAAAAAA求解下列各式的值或解方程。小结：两个排列相同，当且仅当这两个排列的_____完全相同，排列的____也完全相同元素顺序