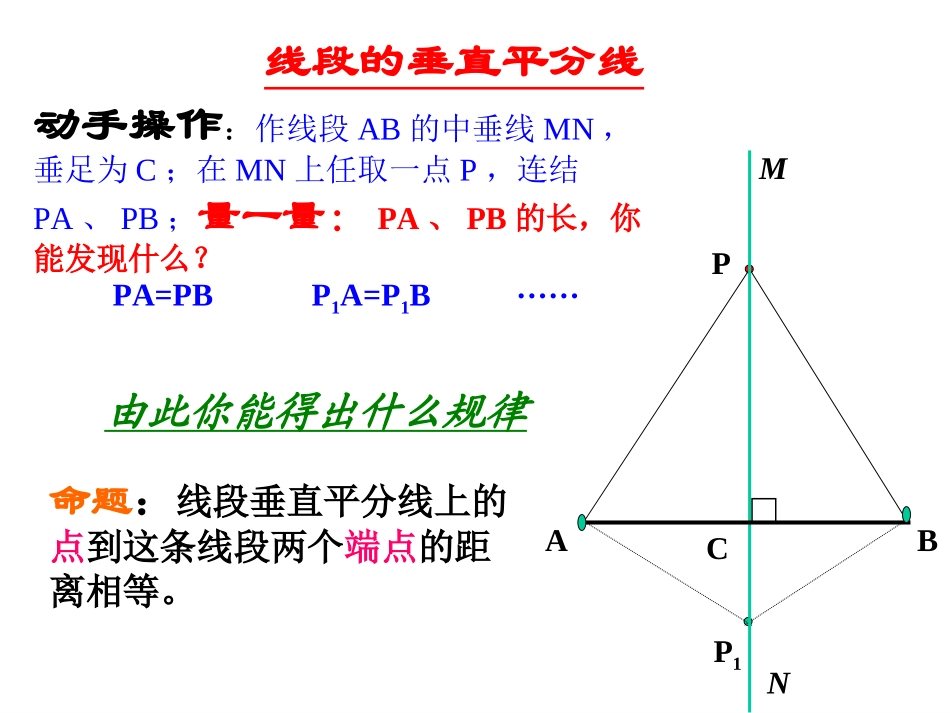
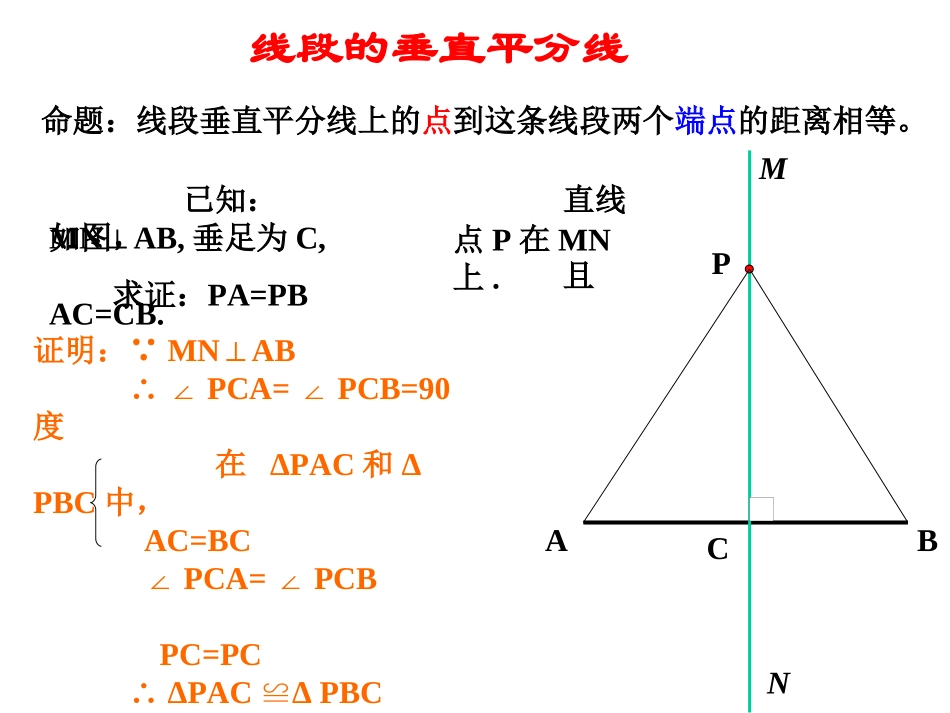
线段的垂直平分线AB线段的垂直平分线PA=PBP1P1A=P1B……命题:线段垂直平分线上的点到这条线段两个端点的距离相等。PMNC动手操作:作线段AB的中垂线MN,垂足为C;在MN上任取一点P,连结PA、PB;量一量:PA、PB的长,你能发现什么?由此你能得出什么规律命题:线段垂直平分线上的点到这条线段两个端点的距离相等。线段的垂直平分线ABPMNCPA=PB直线MNAB,⊥垂足为C,且AC=CB.已知:如图,点P在MN上.求证:证明:∵MNAB⊥∴∠PCA=PCB=90∠度在ΔPAC和ΔPBC中,AC=BC∠PCA=PCB∠PC=PC∴ΔPACΔPBC≌∴PA=PB性质定理:线段垂直平分线上的点到这条线段两个端点的距离相等。线段的垂直平分线ABPMNCPA=PB点P在线段AB的垂直平分线上线段垂直平分线上的点到这条线段两个端点的距离相等几何语言叙述:∵点P在线段AB的垂直平分线上∴PA=PB8课堂练习练习1如图,在△ABC中,BC=8,AB的中垂线交BC于D,AC的中垂线交BC与E,则△ADE的周长等于______.ABCDEPABC已知:如图,PA=PB.求证:点P在线段AB的垂直平分线上.证明:如图作PC⊥AB则∠PCA=∠PCB=90°.在Rt△PCA和Rt△PCB中,∴Rt△PCA≌Rt△PCB(HL).∴AC=BC.又PC⊥AB,∴点P在线段AB的垂直平分线上PA=PB,PC=PC,反过来,如果PA=PB,那么点P是否在线段AB的垂直平分线上呢?点P在线段AB的垂直平分线上.探索并证明线段垂直平分线的判定用几何语言表示为:PABC线段垂直平分线的判定与一条线段两个端点距离相等的点,在这与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.条线段的垂直平分线上.∵PA=PB,∴点P在AB的垂直平分线上.解:∵AD⊥BC,BD=DC∴AD是BC的垂直平分线∴AB=AC∵点C在AE的垂直平分线上∴AC=CE.∴AB=AC=CE课堂练习P622如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上,AB,AC,CE的长度有什么关系?AB+BD与DE有什么关系?ABCDE∵AB=CE,BD=DC,∴AB+BD=CD+CE.即AB+BD=DE.解:∵AB=AC,∴点A在BC的垂直平分线.∵MB=MC,∵点M在BC的垂直平分线上∴直线AM是线段BC的垂直平分线.课堂练习P622练习3如图,AB=AC,MB=MC.直线AM是线段BC的垂直平分线吗?ABCDM(1)任意取一点K,使点K与点C在直线AB两旁.尺规作图经过已知直线外一点作这条直线的垂线。(2)以点C为圆心,CK为半径作弧,交AB于点D和点E.(4)作直线CF,直线CF就是所求作的垂线。CABKFDE已知:直线AB和AB外一点C求作:AB的垂线,使它经过点C.做法:12DE(3)分别以点D和点E为圆心,大于的长为半径作弧,两弧相交于点F.结论:三角形三边垂直平分线交于一点,结论:三角形三边垂直平分线交于一点,这一点到三角形三个顶点的距离相等。这一点到三角形三个顶点的距离相等。你能依据例你能依据例11得到什么结论得到什么结论??例1已知:如图,在ΔABC中,边AB,BC的垂直平分线交于P.求证:点P在AC的垂直平分线上;BACMNM’N’P证明:∵点P在线段AB的垂直平分线MN上,∴PA=PB(?)同理PB=PC.∴PA=PC.∴点P在AC的垂直平分线上;∴AB,BC,AC的垂直平分线相交于点P.已知:如图,在等腰三角形ABC中,腰AB的垂直平线MN交AC于点D,BC=8厘米,ΔBDC的周长20厘米.求:AB的长.ABCDMN已知:如图,D是BC延长线上的一点,BD=BC+AC.求证:点C在AD的垂直平分线上.ABCD8二、逆定理:到线段两个端点距离相等的点,在这条线段的垂直平分线上。线段的垂直平分线一、性质定理:线段垂直平分线上的点到这条线段两个端点的距离相等。PA=PB点P在线段AB的垂直平分线上到线段两个端点距离相等的点,在这条线段的垂直平分线上线段垂直平分线上的点到这条线段两个端点的距离相等返回主页