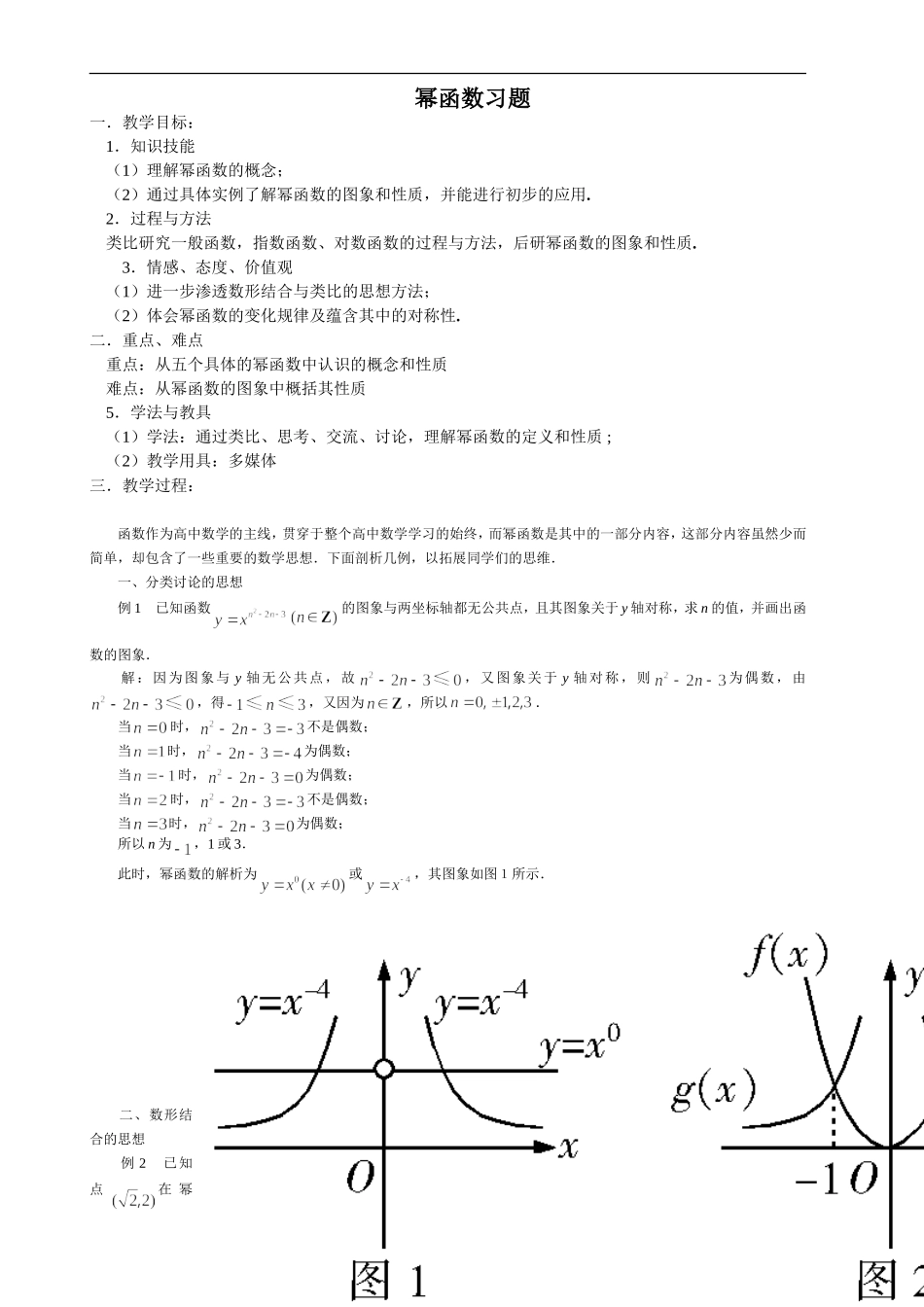
幂函数习题一.教学目标:1.知识技能(1)理解幂函数的概念;(2)通过具体实例了解幂函数的图象和性质,并能进行初步的应用.2.过程与方法类比研究一般函数,指数函数、对数函数的过程与方法,后研幂函数的图象和性质.3.情感、态度、价值观(1)进一步渗透数形结合与类比的思想方法;(2)体会幂函数的变化规律及蕴含其中的对称性.二.重点、难点重点:从五个具体的幂函数中认识的概念和性质难点:从幂函数的图象中概括其性质5.学法与教具(1)学法:通过类比、思考、交流、讨论,理解幂函数的定义和性质;(2)教学用具:多媒体三.教学过程:函数作为高中数学的主线,贯穿于整个高中数学学习的始终,而幂函数是其中的一部分内容,这部分内容虽然少而简单,却包含了一些重要的数学思想.下面剖析几例,以拓展同学们的思维.一、分类讨论的思想例1已知函数的图象与两坐标轴都无公共点,且其图象关于y轴对称,求n的值,并画出函数的图象.解:因为图象与y轴无公共点,故,又图象关于y轴对称,则为偶数,由,得,又因为,所以.当时,不是偶数;当时,为偶数;当时,为偶数;当时,不是偶数;当时,为偶数;所以n为,1或3.此时,幂函数的解析为或,其图象如图1所示.二、数形结合的思想例2已知点在幂1函数的图象上,点,在幂函数的图象上.问当x为何值时有:(1);(2);(3).分析:由幂函数的定义,先求出与的解析式,再利用图象判断即可.解:设,则由题意,得,∴,即.再令,则由题意,得,∴,即.在同一坐标系中作出与的图象,如图2所示.由图象可知:(1)当或时,;(2)当时,;(3)当且时,.小结:数形结合在讨论不等式时有着重要的应用,注意本题中的隐含条件.三、转化的数学思想例3函数的定义域是全体实数,则实数m的取值范围是().A.B.C.D.解析:要使函数的定义域是全体实数,可转化为对一切实数都成立,即且.解得.故选(B)例1已知函数为偶函数,且,求m的值,并确定的解析式.分析:函数为偶函数,已限定了必为偶数,且,,只要根据条件分类讨论便可求得m的值,从而确定的解析式.解:∵是偶函数,∴应为偶数.又∵,即,整理,得,∴,∴.又∵,∴或1.当m=0时,为奇数(舍去);当时,为偶数.故m的值为1,.评注:利用分类讨论思想解题时,要充分挖掘已知条件中的每一个信息,做到不重不漏,才可为正确解题奠定坚实的基础.23