向量的数乘运算及几何意义（课件）詹嘉玲 (2)VIP免费

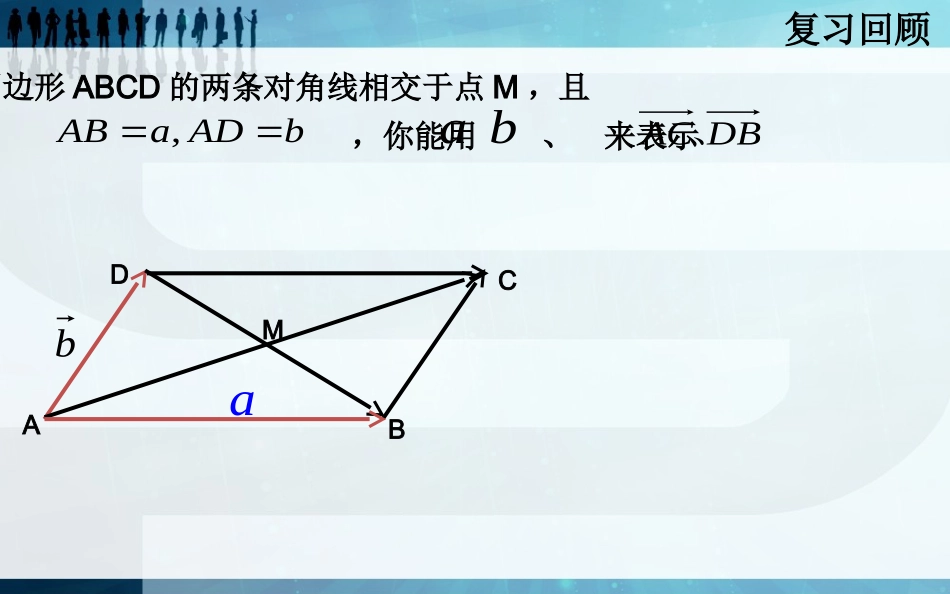
2.2.3向量的数乘运算及几何意义詹嘉玲如图，平行四边形ABCD的两条对角线相交于点M，且，你能用、来表示吗？,ABaADb�abABDCMabDBAC、复习回顾非零向量,作出aaaa及()()()aaaaOaaaABC3aPQaMaNa与方向相同3aa33aa即)(3a与方向相反a)(3a||3|)(3|aaa3讲授新课一般地，我们规定实数λ与向量的积是一个向量，这种运算叫做向量的数乘，记作，它的长度和方向规定如下：aa||||||;aa（1）（2）当时，的方向与的方向相同；当时，的方向与的方向相反。aa0aa0特别的，当时，00.a讲授新课练习1.如图，平行四边形ABCD的两条对角线相交于点M，且，你能用、来表示。,ABaADb�abABDCMabbaADABACAM212121baADABDBDM212121baAMCM21baDMBM21BMCMDMAM、、、52ABC【预习自测】1、（1）点C在线段AB上，且52ACCB，则____ACAB�，____BCAB�.（2）若，6be，则___ba；若，，则.5727－练习2讲授新课向量的数乘运算满足如下运算律：向量的数乘运算满足如下运算律：)();1（（）aa)2)(;(aaa()(3).abab，是实数，a)2(3a)2(3aa6=baba22a2b2baba22)(2ab)(2ba向量的加、减、数乘运算统称为向量的线性运算结合律分配律讲授新课ABCD向量的数乘运算满足如下运算律：向量的数乘运算满足如下运算律：)();1（（）aa)2)(;(aaa()(3).abab，是实数，向量的加、减、数乘运算统称为向量的线性运算结合律分配律(53)(531)ab5533ababb27ab3246abcabc57abc(32)(14)(16)abc20a2、计算：（1）(4)5a；（2）5()3()ababb；（3）(3)2(23)abcabc计算2、计算：（1）；（2）5()3()ababb；（3）(3)2(23)abcabc讲授新课3、问题：（1）若存在实数使得b=a（0a），那么与的位置关系是________；（2）若向量b和（）共线，且=，则当a与b同向时，则=________；当a与b反向时，则=_____。向量共线定理：0.),(,ababa向量与共线当且仅唯一一个当有实数使2)2)为什么要是非零向量为什么要是非零向量??a3)3)可以是零向量吗可以是零向量吗??bab即与共线ba(0)aaa共线3、问题：（1）若存在实数使得=（），那么与的位置关系是________；（2）若向量b和a（0a）共线，且=，则当a与b同向时，则=________；当a与b反向时，则=_____。3、问题：（1）若存在实数使得=（），那么与的位置关系是________；（2）若向量b和（）共线，且=，则当a与b同向时，则=________；当a与b反向时，则=_____。)0(||||ab3、问题：（1）若存在实数使得=（），那么与的位置关系是________；（2）若向量b和（）共线，且=，则当a与b同向时，则b=________；当a与b反向时，则b=_____。3、问题：（1）若存在实数使得=（），那么b与a的位置关系是________；（2）若向量b和（）共线，且=，则当a与b同向时，则=________；当a与b反向时，则=_____。思考思考::1)1)为什么唯一的为什么唯一的??讲授新课向量共线定理：0.),(,ababa向量与共线当且仅唯一一个当有实数使ab即与共线ba(0)a2121212122,-32-2,-2;2,2-13eebeeaeebeeaebeaba）（；）（）（是否共线：与、下列向量baab//,1）（baab//,22）（不共线、，使不存在实数（baab,)3讲授新课共线与求证：，已知，例：如图BCDECEBADA.A3A3.3ABAD共线与BCDEB...