直线的方向向量与平面的法向量VIP免费

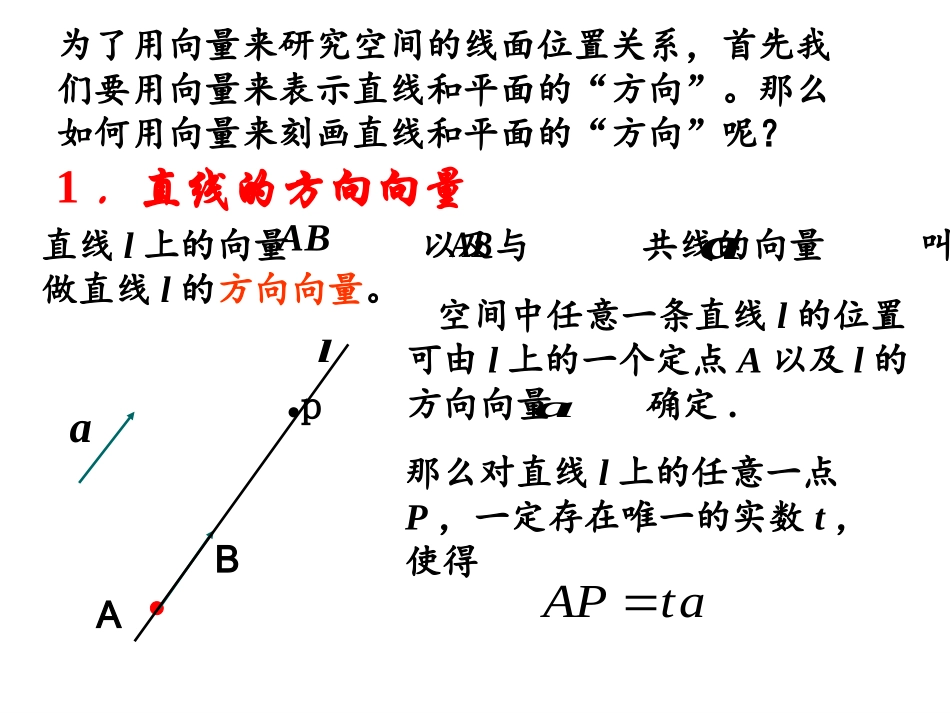
攸县一中洪开科平面向量空间向量推广到立体几何问题(研究的基本对象是点、直线、平面以及由它们组成的空间图形)向量渐渐成为重要工具研究从今天开始,我们将进一步来体会向量这一工具在立体几何中的应用.前面,我们把为了用向量来研究空间的线面位置关系，首先我们要用向量来表示直线和平面的“方向”。那么如何用向量来刻画直线和平面的“方向”呢？1．直线的方向向量aABl直线l上的向量以及与共线的向量叫做直线l的方向向量。AB�aAB�APta�●p空间中任意一条直线l的位置可由l上的一个定点A以及l的方向向量确定.a那么对直线l上的任意一点P，一定存在唯一的实数t，使得由于垂直于同一平面的直线是互相平行的,所以，可以用垂直于平面的直线的方向向量来刻画平面的“方向”。２．平面的法向量平面的法向量：如果直线l⊥α，则l的方向向量叫做平面α的法向量，记作⊥α。uuAul几点注意：1.法向量一定是非零向量;2.一个平面的所有法向量都互相平行;3.向量是平面的法向量，向量是与平面平行或在平面内，则有0auua给定一点A和一个向量,那么过点A以为法向量的平面是确定的.uuabab//abbaba//3．向量在立体几何中的应用abbab0babaaaua//aa或0uauaauuaua//aauv//vuvu//uv0vuvu练习：4.设分别是直线l1,l2的方向向量,根据下列条件,判断l1,l2的位置关系.ba,(1)(2,3,1),(6,9,3)(2)(5,0,2),(0,4,0)ababl1∥l2l1⊥l25.设分别是平面α,β的法向量,根据下列条件,判断α,β的位置关系.vu,1(1)(1,1,2),(3,2,)2(2)(0,3,0),(0,5,0)uvuvα⊥β.α∥β.练习：练习：6.设是直线l的方向向量,是平面α的法向量,根据下列条件,判断l与α的位置关系.a(1)(3,4,2),(2,2,1)(2)(0,8,12),(0,2,3)auauul∥α或lα.l⊥α.例1．在正方体ABCD—A1B1C1D1中，求证：是平面ACD1的法向量.1�DB证明：设正方体棱长为1，如图建立空间直角坐标系D-xyz则A(1,0,0)，C(0,1,0)，D1(0,0,1)1(1,1,0),(1,0,1)ACAD�110,DBACDBAC�11DBAD同理�所以⊥平面ACD1所以是平面ACD1的法向量.1�DB1�DB1(1,1,1)DB�又AB1A1BC1C1DDxyz由两个三元一次方程组成的方程组的解是不惟一的，为方便起见，取x=1较合理。其实平面的法向量不是惟一的。221453(,,),(,,)ABAC�解：uxyz（，，）uABuAC��则，220,4530xyzxyz即212yxz设，解得(1,2,2),u||3u又122(-333ABC平面的单位法向量为，，）例2．已知空间中的三点A(1,-2,0)，B(3,0,1)，C(5,3,3)，求平面ABC的法向量与单位法向量.设平面ABC的法向量为问题：如何求平面的法向量？(1)(,,)uxyz设出平面的法向量为111222(2)(,,),(,,)aabcbabc求出平面内的两个不共线的向量的坐标111222(3)00axbyczuaubaxbycz根据法向量的定义建立方程组(4)设其中一个未知数的值，解方程组，即得一个法向量。平面的法向量不惟一，合理取值即可。例3．在空间直角坐标系内，设平面α经过点P(x0,y0,z0)，平面α的法向量为=(A,B,C)，M(x,y,z)为平面α内任意一点，求x,y,z满足的关系式。u000(,,)PMxxyyzz�，解：0uPM��依题000(,,)(,,)0ABCxxyyzz即000()()()0AxxByyCzz化简得：例4．证明两个平面平行的判定定理：一个平面内的两条交直线与另一个平面平行，则这两个平面平行。已知直线a、b和平面α、β，a,bβ，a∩b=M，a∥α，b∥α，求证：β∥α，证：设直线a、b方向向量分别为，平面α、β的法向量分别为ba,vu,因为a∥α，b∥α,,aubu所以因为a,bβ，a∩b=M，,u所以所以β∥α,v又//,uv所以练习1.已知分别是直线l1,l2的方向向量,两条件中l1、l2的位置关系是().ba,(1)(2,1,2),(6,3,6)(2)(1,2,2),(2,3,2)abab...