直线的方程的几种形式VIP免费

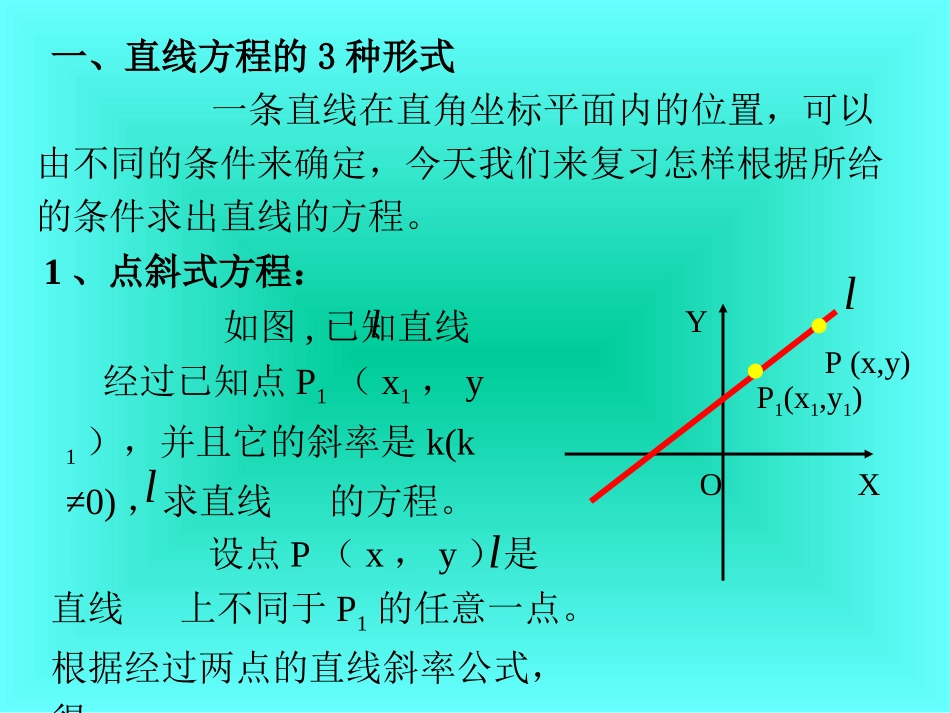
§9－2直线的方程简单回顾上节复习的内容：1、什么叫直线的斜率？2、已知直线l上两个不同点（x1，y1）和（x2，y2），求此直线的斜率。一条直线在直角坐标平面内的位置，可以由不同的条件来确定，今天我们来复习怎样根据所给的条件求出直线的方程。1、点斜式方程：如图,已知直线经过已知点P1（x1，y1），并且它的斜率是k(k≠0)，求直线的方程。ll设点P（x，y）是直线上不同于P1的任意一点。根据经过两点的直线斜率公式，得lOXYP1(x1,y1)l一、直线方程的3种形式P(x,y)11xxyyk1xx可化为可以证明，直线l上的每一个点的坐标都是这个方程的解；反过来，以这个方程的解为坐标的点，都在直线l上，所以，这个方程就是过点P1、斜率为k的直线l的方程。这个方程是由直线上一点和直线的斜率确定的直线方程，所以叫做直线的点斜式方程。OXYP(x,y)p1(x1,y1)l11xxkyy应用：例1：一条直线经过点P1（-2，3），倾斜角α=45°求这条直线的方程，并画出图形。解：这条直线经过点P1(-2，3)，斜率是k=tan45°=1代入点斜式得y－3=x+2，即x－y+5=0·oxy-3-113-55P1(-2，3)·作图：取x=0，代入方程得y=5描点P1(-2，3)与点(0，5)例2.已知直线经过点(2,-7),且它的倾斜角是60°,求直线l方程.解：按所给条件，有,360tan,7,211kyx代入点斜式方程.得),2(3)7(xy化简后得直线方程为.0)732(3yx例3.已知A(1,6)、B(-1,-2)、C(6,3)是三角形的三个顶点，求BC边所在的直线方程.解：设直线BC的斜率为k,则75)1(6)2(31212xxyyk直线BC的点斜式方程是：)1(752xy)6(753xy或2.斜截式方程0xyB(0,b)A(a,0)l如图,直线与x轴交于点A(a,0)与y轴交于点B(0,b)。a叫做直线的横截距.b叫做直线的纵截距.例4已知直线l的斜率为k,纵截距为b,求直线l的方程.代入点斜式方程，得l的直线方程：y－b=k（x－0）即y=kx+b。称为直线的斜截式方程为什么叫斜截式方程？当k≠0时，斜截式方程就是直线的表示形式，这样一次函数中k和b的几何意义就是分别表示直线的斜率和在y轴上的截距．因为它是由直线的斜率和它在y轴上的截距b确定的．解：因为直线l的纵截距为b，即直线l经过点B(0，b).例5、求斜率是5，在y轴上的截距是4的直线方程。解：由已知得k=5，b=4，y=5x+4代入斜截式方程得：即5x-y+4=0例6、求与y轴交于点P(0,6),且倾斜角为45°的直线方程.解：由已知条件，得k=tan45°=1,b=6，代入斜截式方程，得y=x+6例7、一条直线经过点A（0，5），倾斜角为0°，求这直线方程解：这条直线经过点A（0，5）斜率是k=tan0°=0代入点斜式，得y-5=0即y=5.Oxy5:从本例可以看到,00,,111k，yxP直线的斜率时且倾斜角是过点:直线方程是所以，1yy。x，，xl，yl轴的直线方程方程叫做平行于所以轴平行于即直线于上每一点的纵坐标都等上式表示直线1。x轴方程上式又称为所以它的方程为点的横坐标都等于上每一但因用点斜式表示的方程不能因此直线存在这时直线的斜率不时为的倾斜角当直线如果190xl，l，，l，。y轴的直线方程上式又称为平行于0y直线方程为轴的便得到重合于时当特殊地x，y，011xx直线方程为轴的便得到重合于时当特殊地y，x，01。y轴方程称为0xx1点斜式、斜截式不能表示与x轴垂直的直线；与x轴垂直的直线可表示成x=x0，与x轴平行的直线可表示成y=y0。它们都是二元一次方程．我们问：直线的方程都可以写成二元一次方程吗？反过来，二元一次方程都表示直线吗？二、直线方程的一般形式我们知道，在直角坐标系中，每一条直线都有倾斜角α．当α≠90°时，直线有斜率，方程可写成下面的形式：y=kx+b当α=90°时，它的方程可以写成x=x0的形式．由于是在直角坐标平面上讨论问题，上面两种情形得到的方程均可以看成是二元一次方程．这样，对于每一条直线都可以求得它的一个二元一次方程，就是说，直线的方程都可以写成关于x、y的一次方程．反过来，对于x、y的一次方程的一般形式Ax+By+C=0．(1)其中A、B不同时为零．(1)当B≠0时，方程(1)可化为.BCxBAy。BCy，BA的直线轴上截距为且在它表示斜率为(2)当B=0时，由于A、B不同时为零，必有A≠0，方程(1)可化为AC...