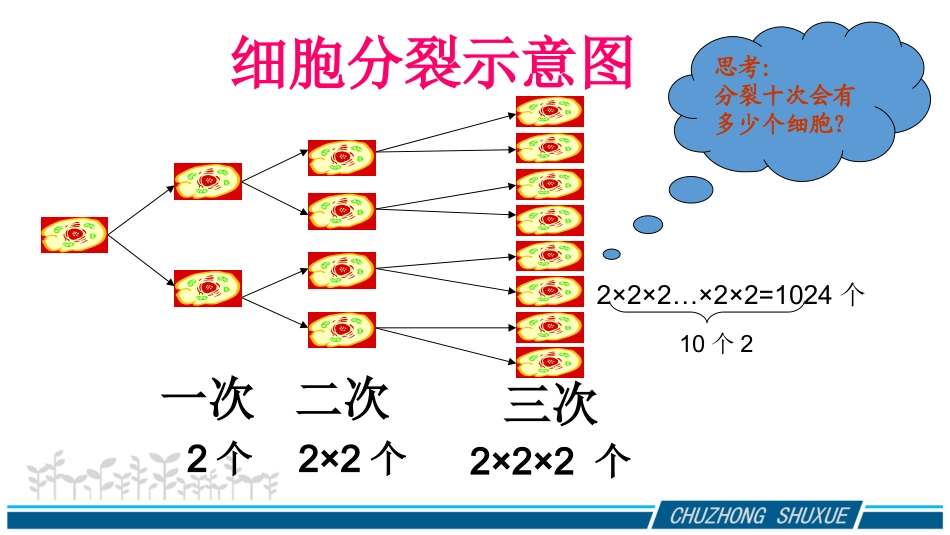
有理数的乘方授课教师:姚金笛数学七年级上某种细胞每过30分钟便由一个分裂成2个,经过5小时,这种细胞由1个能分裂成多少个?一次二次三次细胞分裂示意图2×2×2个2个2×2个思考:分裂十次会有多少个细胞?2×2×2…×2×2=1024个10个22×2×2…×2×210个2=210想一想:思考:a×a×a×......×a相乘应如何表示?n个a2×2×2…×2×2有简单的表示方法吗?10个2学习新知:乘方:求n个相同因数a的积的运算叫做乘方,乘方的结果叫做幂,a叫做底数,n叫做指数,an读作“a的n次幂”(或“a的n次方”)。指数底数幂n个aa×a×…×a=anan一个数可以看作这个数本身的一次方,例如8就是81,通常指数为1时省略不写。乘方是一种特殊的乘法运算1、94的底数是,指数是,表示。942、﹙–2﹚4的底数是,指数是,表示。-243、–24的底数是,指数是,表示。249×9×9×9(-2)×(-2)×(-2)×(-2)-2×2×2×2练习一、理解新知底数是负数和分数时,书写时要把底数用括号括起来探究一、根据乘方的意义判断下列等式是否正确,并思考乘方书写时需要注意哪些问题?1.(-6)×(-6)=-622.03=3×3×33.0.14=0.1×0.1×0.1×0.14.××=5.(-10)3=(-10)×(-10)×(-10)353535335()()()()()××√×√例1、计算解:①53=5×5×5=125②③①)2(43)32(53②(—2)4=(—2)×(—2)×(—2)×(—2)=16③(—)3=(—)×(—)×(—)=—32323232278②③④⑤⑥①练习二、计算322)3(2342)34((-1)441=-9=9=-=1=-1316=916⑴正数的任何次幂都是正数。⑵0的任何正整数次幂都是0。⑶负数的奇次幂是负数,负数的偶次幂是正数。探究二、底数是有理数时,幂的正负有哪些规律?例2.计算:(1)102,103,104,105;(2)(-10)2,(-10)3,(-10)4,(-10)5.(2)(-10)2=100,(-10)3=-1000,(-10)4=10000,(-10)5=-100000.解:(1)102=100,103=1000,104=10000,105=100000;10的几次方就在1的后面加几个0。探究三、观察例2的结果你能发现什么规律?102=100,103=1000,104=10000,105=100000;共同回放:1理解掌握有理数乘方意义,并会正确的计算乘方的结果。2有理数的乘方在书写时需要注意哪些问题。3底数是有理数时幂的正负有哪些规律。410n的规律。⑴基础练习计算:①(—1.2)2;②(-)3;③104;④105;⑤0.14;⑥0.15。分层作业,步步提升65(2)拓展训练①非负性应用:已知(1—m)2+︱n+2︱=0,则m+n=。②规律探索性:21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256………,则22014的末尾数字是。