整数指数幂法则应用-(2)VIP免费

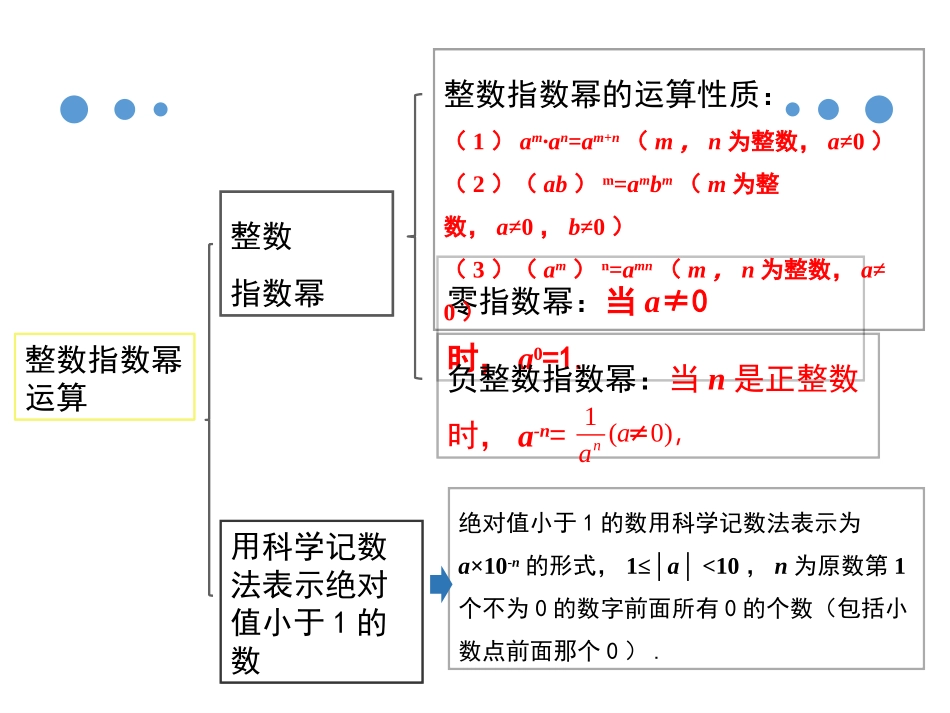
15.2.3整数指数幂的应用第十五章分式整数指数幂运算整数指数幂零指数幂：当a≠0时，a0=1.负整数指数幂：当n是正整数时，a-n=1(0)naa≠，整数指数幂的运算性质：（1）am·an=am+n（m，n为整数，a≠0）（2）（ab）m=ambm（m为整数，a≠0，b≠0）（3）（am）n=amn（m，n为整数，a≠0）用科学记数法表示绝对值小于1的数绝对值小于1的数用科学记数法表示为a×10-n的形式，1≤│a│<10，n为原数第1个不为0的数字前面所有0的个数（包括小数点前面那个0）.用科学记数法表示一些绝对值小于1的数的方法：即利用10的负整数次幂，把一个绝对值小于1的数表示成a×10-n的形式，其中n是正整数，1≤︴a︴<10.n等于原数第一个非零数字前所有零的个数（特别注意：包括小数点前面这个零）.知识要点引入负整数指数幂后，指数的取值范围就推广到全体整数.也就说前面提到的运算性质也推广到整数指数幂.计算：2325212322223(1);(2);(3)();(4)().baaaababab解：2525771(1);aaaaa43622462();bbaaab（）做一做解：6123363(3)();bababa2222322668888(4)().ababababbaba12322223(3)();(4)().ababab学了就用6.75×10－79.9×10－10用科学记数法表示：（1）０.００００００675=（2）０.０００００００００99=（３）-０.００００００００61＝-6.1×10－9用小数表示下列各数：(1)2×10－7；(2)3.14×10－5；(3)7.08×10－3；(4)2.17×10－1.解析：小数点向左移动相应的位数即可．解：(1)2×10－7＝0.0000002；(2)3.14×10－5＝0.0000314；(3)7.08×10－3＝0.00708；(4)2.17×10－1＝0.217.5.比较大小：（1）3.01×10－4_______9.5×10－3（2）3.01×10－4________3.10×10－4<<6.用科学记数法把0.000009405表示成9.405×10n，那么n=.-6课堂达标测试基础题：1.计算：(1)(a+b)m+1·(a+b)n-1;(2)(-a2b)2·(-a2b3)3÷(-ab4)5(3)(x3)2÷(x2)4·x0(4)(-1.8x4y2z3)÷(-0.2x2y4z)÷(-1/3xyz)提高题：2.已知，求a51÷a8的值；0)1(22bab3.计算：xn+2·xn-2÷(x2)3n-3;4.已知：10m=5,10n=4,求102m-3n.