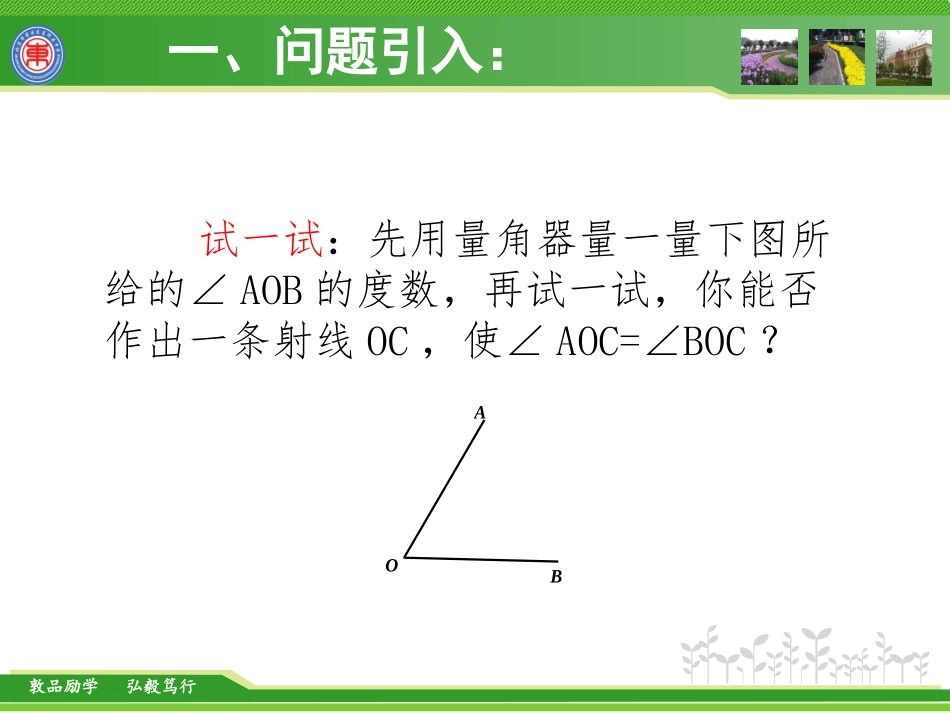
北京出版社义务教育教科书七年级上册数学《3.8角平分线》主讲教师:王晓静单位:北京市密云区东邵渠中学北京市密云区东邵渠中学3.8角平分线北京市密云区东邵渠中学王晓静敦品励学弘毅笃行一、问题引入:试一试:先用量角器量一量下图所给的∠AOB的度数,再试一试,你能否作出一条射线OC,使∠AOC=∠BOC?ABO敦品励学弘毅笃行一、问题引入:角平分线OBAC敦品励学弘毅笃行1.理解角平分线的概念及其表示方法,会进行三种语言的转化;2.会用角平分线的定义进行角度的计算。学习目标敦品励学弘毅笃行1.角平分线的定义:二、新课学习环节一:请试着给角平分线下定义敦品励学弘毅笃行1.角平分线的定义:二、新课学习角平分线:如果经过角的顶点的一条射线把一个角分成相等的两个角,那么这条射线叫做这个角的平分线。环节二:学生展示,教师点拨敦品励学弘毅笃行2.(探究)角平分线的表示:二、新课学习环节一:结合图形,试着写出角平分线的几何语言表示(在导学案上完成)要求:师友独立完成,交流后,准备展示。敦品励学弘毅笃行2.(探究)角平分线的表示:二、新课学习环节二:师友展示。要求:学师指图说出角平分线的几何语言表示。敦品励学弘毅笃行2.(探究)角平分线的表示:二、新课学习教师点拨:已知角平分线,得出三组结论,一个相等,两个2倍,两个.敦品励学弘毅笃行3.例1二、新课学习已知OC是∠AOB的角平分线,若∠AOC=20°,则∠BOC=___°,∠AOB=___°;若∠AOB=50°,则∠BOC=___°,∠AOC=___°。要求:独立完成,师友展示,学友说答案,学师点评依据。20402525敦品励学弘毅笃行4.例2.填空二、新课学习(1)如图1,已知∠1=∠2=∠3=∠4①∵∠1=∠2(已知)∴射线OE是的角平分线();②∵∠3=∠4()∴________().要求:独立完成,师友交流,学友展示。∠AOC角平分线定义已知角平分线定义射线OF是∠COB的角平分线敦品励学弘毅笃行4.例2.填空二、新课学习(1)如图1,已知∠1=∠2=∠3=∠4③∵∠1=∠3∠2=∠4∴∠1+∠2=∠3+∠4即∠AOC=∠BOC∵∠AOC=∠BOC∴()射线OC是∠AOB的角平分线角平分线定义敦品励学弘毅笃行4.例2.填空二、新课学习(2)如图2,∵BD平分∠ABC(已知)∴∠DBC=()∵∠ABC=90°(已知)∴∠DBC=°.∠ABC45角平分线定义敦品励学弘毅笃行4.例2.填空二、新课学习教师点拨:读题标图,联想相关定义或定理的结论,结合已知和所求得出相应的几何语言。敦品励学弘毅笃行1.填空三、互助提高已知:如图,OE平分∠BOC,OD平分∠AOC,∠BOE=20°,∠AOD=40°。则∠BOC=______°,∠DOE=______°要求:先独立完成两道题,师友交流,准备展示。4060敦品励学弘毅笃行2.解答题:三、互助提高已知:如图,OC是∠AOB平分线,∠BOC=20°.求∠AOB的度数。(请试着写出解答过程)敦品励学弘毅笃行2.解答题:三、互助提高教师点拨:1.读题,标图,标到不能标为止;2.根据条件想结论,根据所求找依据。敦品励学弘毅笃行四、总结提升1、本节课你有哪些收获?2、你的师友对你的帮助有哪些?你想对你的师友说……敦品励学弘毅笃行四、总结提升•教师提升:1.角平分线的定义;2.角平分线的几何语言表示(三组结论);3.已知角平分线可以得出角的相等或倍数分数关系,从而求出角的度数。4.数形结合和转化思想;5.类比学习。敦品励学弘毅笃行五、巩固反馈:完成导学案上的检测题目:1.如图,BD平分∠ABC,∠ABD=20°,则∠DBC=°;则∠ABC=°。2.如图,射线OC平分∠AOB。若∠AOB=50°,则∠AOC=______°;若∠BOC=23°,则∠AOB=______°;若∠AOC=24°,则∠BOC=______°.敦品励学弘毅笃行五、巩固反馈:完成导学案上的检测题目:3.如图:∵射线OC是∠AOB的角平分线(已知)∴=∠BOC(角平分线定义)∵射线OD平分∠AOC()∴∠AOD=()∵射线OE是∠BOC的角平分线()∴∠BOC=()敦品励学弘毅笃行六、作业:1.必做题:P141.练习题;2.选做题:P142.提升3,4;3.同步练习:P79.敦品励学弘毅笃行谢谢聆听!