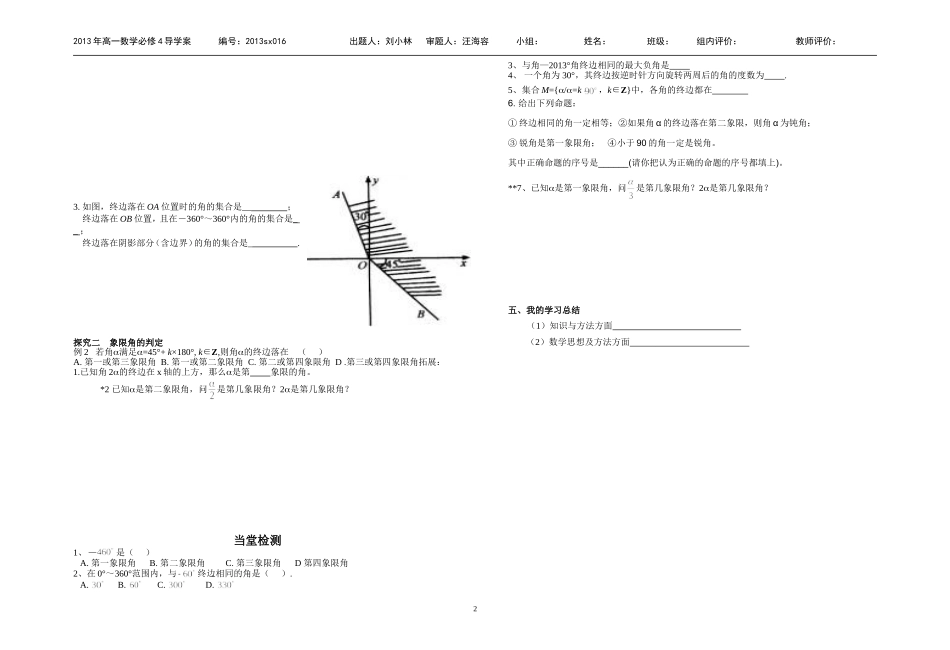
2013年高一数学必修4导学案编号:2013sx016出题人:刘小林审题人:汪海容小组:姓名:班级:组内评价:教师评价:§1.1.1任意角使用说明与学法指导1、用10分钟左右的时间,阅读课本的基础知识,自主高效预习,提升自己的阅读理解能力。2、完成教材助读设置的问题,然后结合课本的基础知识和例题,完成预习自测。3、各组BB级的同学对加**题目不作要求,CC级的同学对加*及**题目不作要求.4、将预习中不能解决的问题标出来,并写到后面“我的疑惑”处。学习目标1.了解正角、负角和零角的概念,理解角的概念的推广;2.掌握终边相同的角的表示方法;3.能够判断任意角所在的象限。.问题导学(预习教材P2~P5,找出疑惑之处)1、角的概念:角可以看成平面内一条绕着从一个位置旋转到另一个位置所成的2、任意大小的角、正角、负角和零角概念:按逆时针方向旋转所形成的角叫角,按顺时针方向旋转所形成的角叫角,未作任何旋转所形成的角叫角.练习:钟表经过4小时,时针与分针各旋转和(填度数).3、如何将角放入坐标系中讨论?角的顶点与重合,角的与轴的重合.角的终边在第几象限,我们就说这个角是第几象限角.在坐标系中表示300°、490°、-330°角,并判别它们分别在第、、象限。4、终边相同的角(1)两角相等,它们的终边位置关系怎么样?两角的终边相同,它们的大小关系呢?(2)与45°终边相同的角有、、、…都可以用代数式表示为.(3)与α角终边相同的角,都可用式子k×360°+α表示,k∈Z,写成集合为:,5、下列说法:①第一象限的角都是锐角;②第二象限角大于第一象限角;③~的角是第一象限角;④小于1800的角是钝角、直角或锐角,其中错误的序号为.6已知角α=—2011°,则与α终边相同的最小正角是.6、完成下表象限角象限角的集合表示第一象限角第二象限角第三象限角第四象限角角终边的位置角的集合表示在轴的非负半轴上在轴的非正半轴上在轴的非负半轴上在轴的非正半轴上在轴上在轴上我的收获我的疑问合作探究探究一终边相同的角例1:在0°~360°间,找出下列终边相同角,并判断它是哪个象限的角:(1)-150°(2)1040°(3)-940°.拓展1:写出与下列终边相同的角的集合,并写出-720°~360°间角,并判断它是哪个象限角.(1)120°(2)-270°(3)1020°.2:写出终边在下列位置上的角的集合:(1)y轴(2)直线y=x(3)第一象限(4)写出终边在直线y=-x上的角的集合.12013年高一数学必修4导学案编号:2013sx016出题人:刘小林审题人:汪海容小组:姓名:班级:组内评价:教师评价:3.如图,终边落在OA位置时的角的集合是__;终边落在OB位置,且在-360°~360°内的角的集合是__;终边落在阴影部分(含边界)的角的集合是_.探究二象限角的判定例2若角满足=45°+k×180°,k∈Z,则角的终边落在()A.第一或第三象限角B.第一或第二象限角C.第二或第四象限角D.第三或第四象限角拓展:1.已知角2的终边在x轴的上方,那么是第象限的角。*2已知是第二象限角,问是第几象限角?2是第几象限角?当堂检测1、是()A.第一象限角B.第二象限角C.第三象限角D第四象限角2、在0°~360°范围内,与终边相同的角是().A.B.C.D.3、与角—2013°角终边相同的最大负角是4、一个角为30°,其终边按逆时针方向旋转两周后的角的度数为.5、集合M={/=k,k∈Z}中,各角的终边都在6.给出下列命题:①终边相同的角一定相等;②如果角α的终边落在第二象限,则角α为钝角;③锐角是第一象限角;④小于90的角一定是锐角。其中正确命题的序号是______(请你把认为正确的命题的序号都填上)。**7、已知是第一象限角,问是第几象限角?2是第几象限角?五、我的学习总结(1)知识与方法方面(2)数学思想及方法方面2