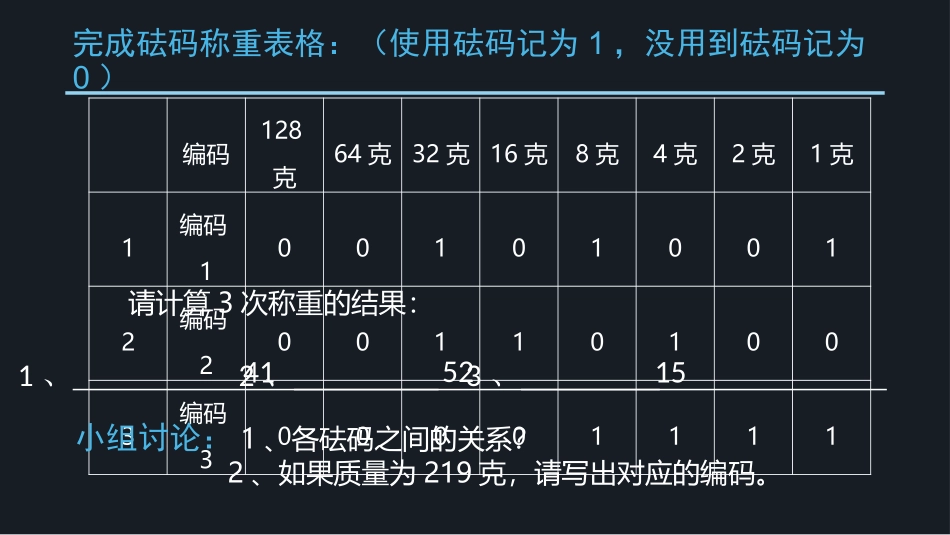
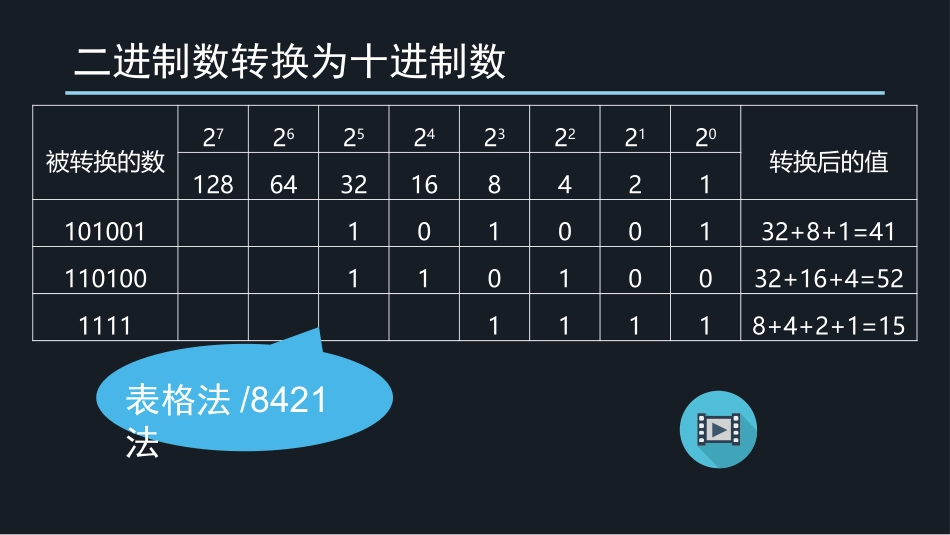
不同数制的相互转换孙力威2016.9.13完成砝码称重表格:(使用砝码记为1,没用到砝码记为0)编码128克64克32克16克8克4克2克1克1编码1001010012编码2001101003编码300001111请计算3次称重的结果:1、3、2、小组讨论:1、各砝码之间的关系?2、如果质量为219克,请写出对应的编码。415215二进制数转换为十进制数被转换的数2726252423222120转换后的值128643216842110100110100132+8+1=4111010011010032+16+4=52111111118+4+2+1=15表格法/8421法二进制数转换为十进制数基本方法:按权展开,累加求和完成砝码称重表格:(使用砝码记为1,没用到砝码记为0)编码128克64克32克16克8克4克2克1克1编码1001010012编码2001101003编码300001111请计算3次称重的结果:1、3、2、小组讨论:1、各砝码之间的关系?2、如果质量为219克,请写出对应的编码。415215十进制数转换为二进制数被转换的数2726252423222120转换后的值12864321684212191101101111011011表格法表格法:实现二进制与十进制间的互换。十进制数转换为二进制数基本方法:除二取余法将20转换为二进制数202100205221210201直到商为0由下到上按顺序写出:10100十进制与二进制相互转换练习1111010122小结二进制十进制1.表格法/8421法2.按权展开,累加求和1.表格法2.除以2取余,倒序排列十进制转换为十六进制/八进制???尝试一下,把十六进制和八进制转换为十进制:36H=D(36)8=D提示:二进制转换为十进制是用按权展开,累加求和的方法。十进制与N进制数的相互转换5430N进制转换为十进制数:按权展开,累加求和十进制与N进制数的相互转换提示:十进制转二进制是除以2取余。(245)10=()8F5365十进制转换为N进制数:除以N取余和八进制二进制转换为十六进制/八进制???十六进制与二进制的对应关系:十进制0123456789101112131415十六进制二进制二进制数转换为十六进制数二进制数转换为十六进制数:把二进制数从右向左按4位一组划分,每组用一位十六进制数表示。1101101011101111101110713D66D7十六进制数大大的缩短了原来二进制数的长度十六进制数转换为二进制数把十六进制数从右向左按每一位十六进制数化为4位的二进制数,按顺序排列即可。注意:除了左边第一位,后面不足四位的必须用“0”补足四位,并且不能省略。12E111000100001000100101110100101110十六进制与二进制相互转换练习1010110110B=H10111011001B=H2B65D94CH=B3B6H=B10011001110110110二进制数转换为八进制数十进制01234567八进制01234567二进制八进制数与二进制数的转换,参照二进制与十六进制的转换,只是将其中的4位变为3位八进制与二进制相互转换练习1010110110B=()810111011001B=()812662731(57)8=B(364)8=B10111111110100不同数制的相互转换二进制十六进制八进制十进制N进制转换为十进制:按权展开,累加求和十进制转换为N进制:除以N取余,倒序排列四合一法一分为四法一分为三法三合一法