4.3相似三角形VIP免费

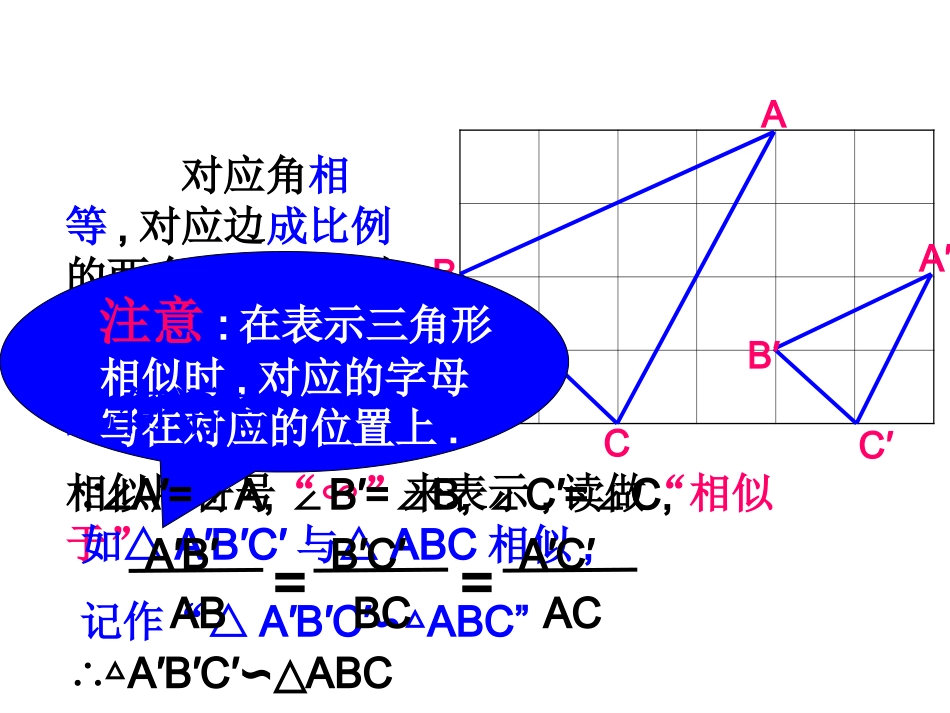
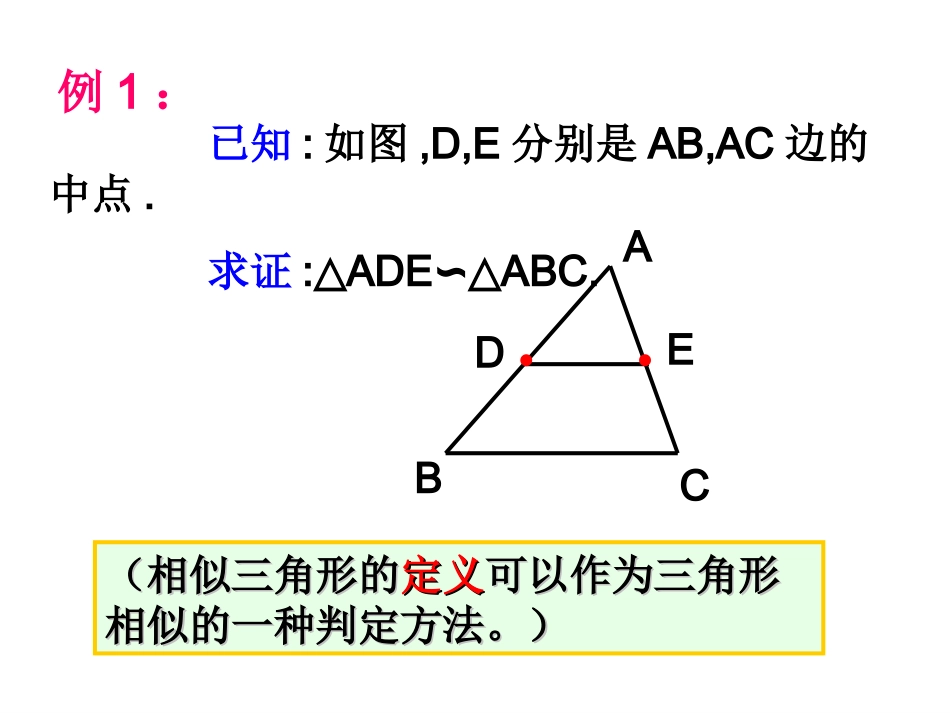
4.3相似三角形CABB′A′C′对应角相等,对应边成比例的两个三角形,叫做相似三角形.相似用符号“∽”来表示,读做“相似于”如△A′B′C′与△ABC相似,记作“△A′B′C′ABC∽△”注意:在表示三角形相似时,对应的字母写在对应的位置上.几何语言:∵∠A′=A,B′=B,C′=C,∠∠∠∠∠ABA′B′BCB′C′ACA′C′==∴△A′B′C′ABC∽△已知:如图,D,E分别是AB,AC边的中点.求证:ADEABC.△∽△EDCBA例1：（相似三角形的（相似三角形的定义定义可以作为三角形可以作为三角形相似的一种判定方法。）相似的一种判定方法。）下图中△ABC与△DEF相似，你能确定出m与x的值吗？30°50°1610.4ABCm°F50°100°8xDE那么△ABC与△DEF对应边的比=？？2816DFAC相似三角形对应边的比,叫做两个相似三角形的相似比即:△ABC与△DEF的相似比=2△DEF与△ABC的相似比=21注意:两个三角形的前后次序，所得的相似比也不同已知△ABC∽△DEF，AC=16cm，DF=8cm１、两个全等三角形一定相似吗？为什么？２.两个直角三角形一定相似吗？为什么？两个等腰直角三角形呢？３.两个等腰三角形一定相似吗？为什么？两个等边三角形呢？(1)BCDEFA题3BCDEFA3045(2)1.相似.因为对应角相等,对应边成比例.２.两个直角三角形不一定相似.因为对应角不一定相等,对应边也不一定成比例;两个等腰直角三角形相似.因为对应角相等,对应边成比例.３.两个等腰三角形不一定相似;两个等边三角形相似.例2、如图(1),D,E分别是△ABC的边BA,CA的延长线上的点,点D与点B是对应点.△ADE∽△ABC。请你找到这两个三角形的对应角、对应边。AEDCB图1已知ADAB=12﹕﹕,BC=9cm,求DE的长.变式1、如图(2),D,E分别是△ABC的边AB,AC上的点,点D与点B是对应点.△ADE∽△ABC.请你找到这两个三角形的对应角、对应边。ADEBC图2已知ADDB=12﹕﹕,BC=9cm,求DE的长。变式2：如图(3),D,E分别是△ABC的AB,AC边上的点，△ADE∽△ACB.∠ADE＝∠CADEBC图3AD＝2cm,DB＝4cm,AC＝10cm,求AE的长.变式3、如图(4),D是△ABC的边AB上的点,ACDABC.△∽△ACD∠＝∠B已知:AD＝9cm,BD＝7cm,求AC的长.ADCB图4变式4、如图(5),D、E分别是△ABC的边BA、CA延长线上的点,点D与点C是对应点.ADEACB.△∽△AD＝2cm,AB＝6cm,AC＝4cm,求AE的长.ADEBC图5已知△ABC与△DEF相似,ABC△的三边为2,3,4,DEF△的最大边为8,求其余两边.已知△ABC与△DEF相似,ABC△的三边为2,3,4,DEF△的一边为8,求其余两边.4,64,6或12,16或16/3,32/3梳理知识对应角对应边记法定义对应角相等、对应边相等的两个三角形叫做全等三角形。对应角相等对应边相等△ABCDEF≌对应边成比例对应角相等对应角相等、对应边成比例的两个三角形叫做相似三角形△ABC∽DEF全等三角形是相似三角形的特殊情形（相似比为1）相似三角形