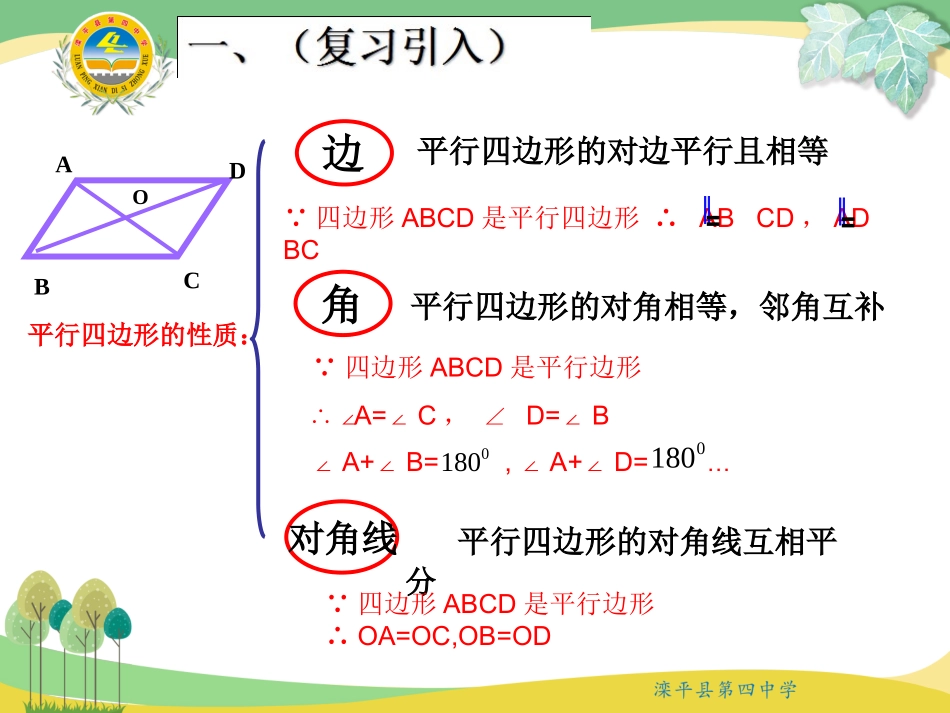
边平行四边形的对边平行且相等角对角线平行四边形的对角线互相平分平行四边形的性质:BDACO∵四边形ABCD是平行四边形∴ABCD,ADBC∥﹦∥﹦平行四边形的对角相等,邻角互补∵四边形ABCD是平行边形∴∠A=∠C,∠D=∠B∠A+∠B=,∠A+∠D=…01800180∵四边形ABCD是平行边形∴OA=OC,OB=OD学习目标•1.在探索平行四边形判定定理的基础上,会证明平行四边形的判定定理1。•2.掌握平行四边形的判定定理1及其应用。BDAC→边一组对边平行一组对边相等一组对边平行且相等一组对边平行另一组对边相等两组对边分别平行两组对边分别相等(×)(×)(×)(√)二、自主探究交流展示画两条互相平行的直线,在这两条直线上分别截取线段AB=CD,连接AD,BC,得四边形ABCD。动手画一画(1)你认为这样得到的四边形ABCD是不是平行四边形?(2)由此,你发现了什么结果?验证你的猜想要求:(1)请你用已画好的平行四边形;(2)通过小组合作,对四边形ABCD是平行四边形进行说理;(3)展示:请尝试着有条理的表达自己的证明思路。(要求声音洪亮)BDAC→边一组对边平行一组对边相等一组对边平行且相等一组对边平行另一组对边相等两组对边分别平行(×)(×)(×)(√)二、自主探究交流展示(√)平行四边形的判定定理1一组对边平行且相等平行且相等的四边形是平行四边形。根据文字命题画出图形,用符号语言写出已知、求证。BDCA已知:如图,在四边形ABCD中,AD∥BC,AD=BC求证:四边形ABCD是平行四边形.一组对边平行且相等平行且相等的四边形是平行四边形。证明:如图,连接BD。在△ABD和△CDB中,∵ADBC∥∴∠ADB=CBD∠∵AD=CB,BD=DB∴△ABDCDB≌△∴∠ABD=CDB∠∴ABDC∥∴四边形ABCD是平行四边形.平行四边形的判定定理1一组对边平行且相等平行且相等的四边形是平行四边形。ABCD几何语言:∵AD//BC,AD=BC∴四边形ABCD是平行四边形(一组对边平行且相等的四边形是平行四边形)已知:如图所示,在▱ABCD中,E为BA延长线上一点,F为DC延长线上一点,且AE=CF,连接BF,DE.求证:四边形BFDE是平行四边形.证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD.又∵AE=CF,∴BE=BA+AE=DC+CF=DF,且BE∥DF.∴四边形BFDE是平行四边形.EABFCD三、典例分析四、跟踪训练1.如图所示,在四边形ABCD中,AB∥CD,请你添加一个条件,使得四边形ABCD成为平行四边形,并说明理由。ADBC2.如图所示,在四边形ABCD中,∠B=∠D,∠BAC=∠DCA.求证:四边形ABCD是平行四边形.ADBC3.如图所示,E,F是四边形ABCD的对角线AC上的两点,AD∥BC,DF∥BE,AE=CF.求证:四边形ABCD是平行四边形.证明:(1)∵AD∥BC,∴∠1=∠2.∵DF∥BE,∴∠3=∠4.又AE=CF,∴AE+EF=CF+EF,即AF=CE.在△AFD与△CEB中,12,,34,AFCE∴△AFD≌△CEB(ASA).∴AD=CB.又∵AD∥BC,∴四边形ABCD是平行四边形.五、回顾反思感悟提升五、回顾反思感悟提升这节课我们研究了平行四边形什么问题?这节课我们经历了一个怎样的探究过程?11224433通过我们的学习,对我们的后续学习生活有什么启示?教师寄语: